3．两个靠近的天体称为双星，它们以两者连线上某点O为圆心做匀速圆周运动，其质量分别为m₁、m₂，如图所示，以下说法正确的是（　　）

	A．	它们的角速度与半径成反比
	B．	它们的线速度与半径成正比
	C．	向心力与它们质量的乘积成正比
	D．	它们各自做匀速圆周运动的轨道半径与质量成反比

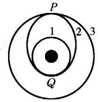2．如图所示，发射地球同步卫星时，先将卫星发射至近地圆轨道1，然后经点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送入同步轨道3．轨道1、2相切于Q点，轨道2、3相切于P点（如图所示），则当卫星分别在1、2、3轨道正常运行时，以下说法正确的是（　　）

	A．	卫星在轨道3上的速度大于在轨道1上的速度
	B．	卫星在轨道3上的角速度小于在轨道1上的角速率
	C．	卫星在轨道2上经过Q点时的速度大于它在轨道2上经过P点时的速度
	D．	卫星在轨道1上经过Q点时的加速度小于它在轨道2上经过Q点时的加速度

1．“嫦娥三号”探月卫星于2013年12月2日凌晨在西昌卫星发射中心发射，将实现“落月”的新阶段．若已知引力常量为G，月球绕地球做圆周运动的半径为r₁、周期为T₁，“嫦娥三号”探月卫星做圆周运动的环月轨道半径为r₂、周期为T₂，不计其他天体的影响，根据题目条件可以（　　）

	A．	求出月球的质量		B．	求出“嫦娥三号”探月卫星的质量
	C．	得出$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$		D．	求出地球的密度

20．石墨烯设近些年发现的一种新材料，其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化，其发现者由此获得2010年诺贝尔物理学奖．用石墨烯制作超级缆绳，人类搭建“太空电梯”的梦想有望在本世纪实线．科学家门设想，在地球同步卫星轨道上，建一个同步轨道站，然后垂下一条缆绳直接和地面上的赤道基站连接在一起，让电梯仓沿着这条缆绳运行，就能实现外太空和地球之间便捷的物资交换（地面附近重力加速度为g，地球自转角速度为ω，地球半径R，电梯仓和缆绳的质量远远小于同步轨道站的质量）．
（1）同步轨道站和赤道基站可以看成质点，求缆绳的长度．
（2）当电梯仓沿着缆绳升到离地面为R的位置时，电梯仓停下来，求此时质量为m的物体对电梯底平面的压力大小．

19．假设某星球的质量约为地球质量的9倍，半径约为地球的一半．不考虑星球和地球自转的影响，由以上数据可推算出：
（1）该星球表面重力加速度与地球表面重力加速度之比约为多少？
（2）靠近该星球表面沿圆轨道运行的航天器线速度与靠近地球表面沿圆轨道运行的航天器线速度之比约为多少？
（3）靠近该星球表面沿圆轨道运行的航天器的周期与靠近地球表面沿圆轨道运行的航天器的周期之比约为多少？

18．为了计算地球的质量必须知道一些数据，下列各组数据加上已知的万有引力常量为G，可以计算地球质量的是（　　）

	A．	地球绕太阳运行的周期T和地球离太阳中心的距离R
	B．	月球绕地球运行的周期T和月球离地球中心的距离R
	C．	人造地球卫星在地面附近运行的速度v和运行周期T
	D．	地球自转周期T和地球的平均密度ρ

17．人造地球卫星A和B，它们的质量之比为m_A：m_B=1：2，它们的轨道半径之比为2：1，则下面的结论中正确的是（　　）

	A．	它们受到地球的引力之比为FA：FB=1：1
	B．	它们的运行速度大小之比为vA：vB=1：$\sqrt{2}$
	C．	它们的运行周期之比为TA：TB=$\sqrt{2}$：1
	D．	它们的运行角速度之比为ωA：ωB=3$\sqrt{2}$：1

16．利用如下数据：
地球绕太阳公转的周期T=365天
地球绕太阳公转的轨道半径r=1.5×10¹¹m
地球表面的重力加速度g=9.8m/s²
地球自身的半径R=6.4×10⁶m
估算：太阳质量与地球质量的比值$\frac{{M}_{x}}{Me}$为多少？（结果用科学计数法表示，保留一位有效数字）

15．已知地球的半径为R、表面重力加速度为g，月球绕地球圆周运动的轨道半径为nR、周期为T，则月球运动的向心加速度可表示为（　　）

A．

$（\frac{2π}{T}）^{2}nR$

B．

（$\frac{2π}{T}$）2R

C．

$\frac{g}{{n}^{2}}$

D．

$\frac{g}{n}$

14．一宇航员登陆到某星球上，若知道星球的质量为地球的2倍，直径也为地球的2倍，宇航员在地球上受到的万有引力大小为F，则他在该星球上受到的万有引力大小为（　　）

A．

F

B．

2F

C．

$\frac{F}{2}$

D．

$\frac{F}{4}$