
科目: 来源: 题型:
【题目】如图所示,两物块A、B套在水平粗糙的CD杆上,并用不可伸长的轻绳连接,整个装置能绕过CD中点的轴OO1转动,已知两物块质量相等,杆CD对物块A、B的最大静摩擦力大小相等,开始时绳子处于自然长度(绳子恰好伸直但无弹力),物块B到OO1轴的距离为物块A到OO1轴的距离的两倍,现让该装置从静止开始转动,使转速逐渐增大,在从绳子处于自然长度到两物块A、B即将滑动的过程中,下列说法正确的是( )

A. A受到的静摩擦力一直增大
B. B受到的静摩擦力先增大,后保持不变
C. A受到的静摩擦力是先增大后减小
D. A受到的合外力一直在增大
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,A、B、C三个小球分别从斜面的顶端以不同的速度抛出,其中A、B落到斜面上,C落到水平面上,A、B落到斜面上时速度方向与水平方向的夹角分别为α、β,C落到水平面上时速度方向与水平方向的夹角为γ,则

A. α=β=γ B. α=β>γ C. α=β<γ D. α<β<γ
查看答案和解析>>
科目: 来源: 题型:
【题目】均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m。将其置于磁感应强度为B的水平匀强磁场上方h处,如图所示。线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界面平行。当cd边刚进入磁场时:
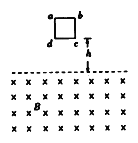
(1)求线框中产生的感应电动势大小;
(2)求cd两点间的电势差大小;
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件。
查看答案和解析>>
科目: 来源: 题型:
【题目】宋代诗人陈与义乘小船出游,曾写下诗句“卧看满天云不动,不知云与我俱东”。诗中描述“云不动”是以______为参考系,“云与我俱东”是以_______为参考系。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,一小球质量为m,用长为L的悬线固定于O点正下方![]() 处钉有一根长钉,把悬线沿水平方向拉直后无初速度地释放小球,当悬线碰到钉子的瞬间,下列说法错误的是
处钉有一根长钉,把悬线沿水平方向拉直后无初速度地释放小球,当悬线碰到钉子的瞬间,下列说法错误的是
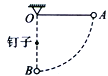
A. 小球的向心加速度突然增大
B. 小球的角速度突然增大
C. 小球的速度突然增大
D. 悬线的张力突然增大
查看答案和解析>>
科目: 来源: 题型:
【题目】假设地球是一半径为R、质量分布均匀的球体。一矿井深度为d.已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的重力加速度大小之比为
A. 1-![]() B. 1+
B. 1+![]() C. (
C. (![]() )2 D. (
)2 D. (![]() )2
)2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,一个质量为m的圆环套在一根固定的水平长直杆上,环与杆的动摩擦因数为μ.现给环一个向右的初速度v0,同时对环施加一个竖直向上的作用力F,并使F的大小随v的大小变化,两者的关系为F=kv,其中k为常数,则环运动过程中的v-t图象可能的是


查看答案和解析>>
科目: 来源: 题型:
【题目】一个质量为m的木块,从半径为R、质量为M的1/4光滑圆槽顶端由静止滑下。在槽被固定和可沿着光滑平面自由滑动两种情况下,如图所示,木块从槽口滑出时的速度大小之比为多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】根据玻尔理论,电子绕氢原子核运动可以看作是仅在库仑引力作用下的匀速圆周运动,已知普朗克常数h,真空中光速为c,电子的电荷量为e,质量为m,电子在第1轨道运动的半径为r1,静电力常量为k.
氢原子在不同的能量状态,对应着电子在不同的轨道上绕核做匀速圆周运动,电子做圆周运动的轨道半径满足rn=n2r1,其中n为量子数,即轨道序号,rn为电子处于第n轨道时的轨道半径。电子在第n轨道运动时氢原子的能量En为电子动能与“电子-原子核”这个系统电势能的总和。理论证明,系统的电势能Ep和电子绕氢原子核做圆周运动的半径r存在关系:Ep=-k![]() (以无穷远为电势能零点)。请根据以上条件完成下面的问题。
(以无穷远为电势能零点)。请根据以上条件完成下面的问题。
①试证明电子在第n轨道运动时氢原子的能量En和电子在第1轨道运动时氢原子的能量E1满足关系式![]()
②假设氢原子甲核外做圆周运动的电子从第2轨道跃迁到第1轨道的过程中所释放的能量,恰好被量子数n=4的氢原子乙吸收并使其电离,即其核外在第4轨道做圆周运动的电子脱离氢原子核的作用范围。不考虑电离前后原子核的动能改变,试求氢原子乙电离后电子的动能。
③氢原子光谱中巴耳末系的谱线波长公式为: ![]() ,n = 3、4、5…,请根据玻尔理论推导巴耳末公式并确定里德堡常数R的表达式。
,n = 3、4、5…,请根据玻尔理论推导巴耳末公式并确定里德堡常数R的表达式。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(甲)所示,长为l、相距为d的两块正对的平行金属板AB和CD与一电源相连(图中未画出电源),B、D为两板的右端点。两板间电势差的变化如图(乙)所示。在金属板B、D端的右侧有一与金属板垂直的荧光屏MN,荧光屏距B、D端的距离为l。质量为m,电荷量为e的电子以相同的初速度v0从极板左边中央沿平行极板的直线OO′连续不断地射入。已知所有的电子均能够从两金属板间射出,且每个电子在电场中运动的时间与电压变化的周期相等。忽略极板边缘处电场的影响,不计电子的重力以及电子之间的相互作用。求:
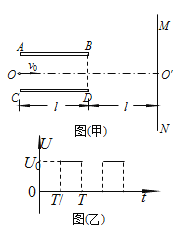
(1)t=0和t=T/2时刻进入两板间的电子到达金属板B、D端界面时偏离OO′的距离之比。
(2)两板间电压的最大值U0。
(3)电子在荧光屏上分布的最大范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com