
科目: 来源: 题型:
【题目】如图所示,为三个有界匀强磁场,磁感应强度大小均为B,方向分别垂直纸面向外、向里和向外,磁场宽度均为L,在磁场区域的左侧边界处,有一边长为L的正方形导体线框,总电阻为R,且线框平面与磁场方向垂直,现用外力F使线框以速度v匀速穿过磁场区域,以初始位置为计时起点,规定电流沿逆时针方向时的电动势E为正,外力F向右为正.则以下能反映感应电动势E和外力F随时间变化规律的图象是( )

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m,电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔s1处射入电容器,穿过小孔s2后从距三角形A点![]() a的P处垂直AB方向进入磁场,试求:
a的P处垂直AB方向进入磁场,试求:

(1)粒子到达小孔s2时的速度和从小孔s1运动到s2所用的时间;
(2)若粒子从P点进入磁场后经时间t从AP间离开磁场,求粒子的运动半径和磁感应强度的大小;
(3)若粒子能从AC间离开磁场,磁感应强度应满足什么条件?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端与小球相连,另一端固定于O点。现将小球从A点由静止释放,沿竖直杆运动到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹力大小相等.在小球由A到B的过程中( )

A. 在B点的速度可能为零
B. 加速度等于重力加速度g的位置有两个
C. 机械能先减小,后增大
D. 弹簧弹力对小球所做的正功等于小球克服弹簧弹力所做的功
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,边长为L、匝数为N,电阻不计的正方形线圈abcd在磁感应强度为B的匀强磁场中绕转轴OO′转动,轴OO′垂直于磁感线,在线圈外接一含有理想变压器的电路,变压器原、副线圈的匝数分别为n1和n2.保持线圈以恒定角速度ω转动,下列判断正确的( )
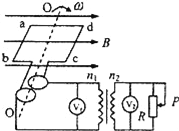
A. 在图示位置时线框中磁通量为零,感应电动势最大
B. 当可变电阻R的滑片P向上滑动时,电压表V2的示数变大
C. 电压表V1示数等于NBωL2
D. 变压器的输入与输出功率之比为1:1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,一质量为m1的木箱放在水平地面上,一个质量为m2的人站在木箱里双手用力向上推木箱,推力为F,结果木箱和人仍静止不动,已知重力加速度为g,则( )

A. 人对木箱底部的压力大小为m2g
B. 人对木箱底部的压力大小为m2g+F
C. 木箱对地面的压力大小为m1g+m2g-F
D. 地面对木箱的支持力大小为m1g+m2g+F
【答案】B
【解析】试题分析:以人为研究对象,人受重力![]() 、木箱对他的支持力
、木箱对他的支持力![]() 和木箱对他的压力F。人处于静止状态,由平衡条件
和木箱对他的压力F。人处于静止状态,由平衡条件![]() ,由牛顿第三定律可知人对木箱的压力
,由牛顿第三定律可知人对木箱的压力![]() ,故B对A错。以整体为研究对象,受力情况为重力、地面对整体的支持力
,故B对A错。以整体为研究对象,受力情况为重力、地面对整体的支持力![]() ,由于整体静止,由平衡条件
,由于整体静止,由平衡条件![]() ,故CD错。故选B。
,故CD错。故选B。
考点:静态平衡问题。
【名师点睛】静态平衡问题也需先进行受力分析,然后根据平衡条件列出平衡方程。联立求解即可。但本题涉及两个物体,所以同学们要灵活选取研究对象,AB选项中的力为人受力,故以人为研究对象。CD中力为整体受力,故选整体为研究对象。
【题型】单选题
【结束】
136
【题目】“太极球”运动是一项较流行的健身运动.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,太极球却不会掉到地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让小球在竖直面内始终不脱离平板且做匀速圆周运动,则( )

A. 小球的机械能保持不变
B. 平板对小球的弹力在A处最小,在C处最大
C. 在B、D两处小球一定受到沿平板向上的摩擦力
D. 只要平板与水平面的夹角合适,小球在B、D两处可能不受平板的摩擦力作用
查看答案和解析>>
科目: 来源: 题型:
【题目】传送带被广泛应用与各行各业,由于不同的物体与传送带之间的动摩擦因数不同,物体在传送带上的运动情况也有所不同。如图所示,一倾斜放置的传送带与水平面的倾角![]() ,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行。M、N为传送带的两个端点,MN两点间的距离L=7m。N端有一离传送带很近的挡板P可将传送带上的物块挡住。在传送带上的O处先后由静止释放金属块A和木块B,金属块与木块质量均为1kg,且均可视为质点,OM间距离LOM=3m。g取10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦。
,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行。M、N为传送带的两个端点,MN两点间的距离L=7m。N端有一离传送带很近的挡板P可将传送带上的物块挡住。在传送带上的O处先后由静止释放金属块A和木块B,金属块与木块质量均为1kg,且均可视为质点,OM间距离LOM=3m。g取10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦。

(1)金属块A由静止释放后沿传送带向上运动,经过![]() 到达M端,求金属块与传送带间的动摩擦因数
到达M端,求金属块与传送带间的动摩擦因数![]() 。
。
(2)木块B由静止释放后沿传送带向下运动,并与挡板P发生碰撞。已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,木块B与传送带间的动摩擦因数![]() 。求:
。求:
a、与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离;
b、经过足够长时间,电动机的输出功率恒定,求此时电动机的输出功率。
查看答案和解析>>
科目: 来源: 题型:
【题目】万有引力定律揭示了天体运行规律与地上物体运动规律具有内在的一致性.
(1)用弹簧秤称量一个相对于地球静止的小物体的重量,随称量位置的变化可能会有不同的结果.已知地球质量为M,自转周期为T,万有引力常量为G.将地球视为半径为R、质量均匀分布的球体,不考虑空气的影响.设在地球北极地面称量时,弹簧秤的读数为F0.
a.若在北极上空高出地面h处称量,弹簧秤读数为F1,求比值![]() 的表达式,并就h=1.0%R的情形算出具体数值(计算结果保留2位有效数字);
的表达式,并就h=1.0%R的情形算出具体数值(计算结果保留2位有效数字);
b.若在赤道地面称量,弹簧秤读数为F2,求比值![]() 的表达式.
的表达式.
(2)设想地球绕太阳公转的圆周轨道半径r、太阳的半径为RS和地球的半径R三者均减小为现在的1.0%,而太阳和地球的密度均匀且不变,仅考虑太阳和地球之间的相互作用,以现实地球的1年为标准,计算“设想地球”的1年将变为多长?
查看答案和解析>>
科目: 来源: 题型:
【题目】二十一世纪,能源问题是全球关注的焦点问题.从环境保护的角度出发,电动汽车在近几年发展迅速.下表给出的是某款电动汽车的相关参数:
参数指标 | 整车质量 | 0~100km/h 加速时间 | 最大速度 | 电池容量 | 制动距离(100km/h~0) |
数值 | 2000kg | 4.4s | 250km/h | 90kWh | 40m |
请从上面的表格中选择相关数据,取重力加速度g=10m/s2,完成下列问题:
(1)求汽车在(100km/h~0)的制动过程中的加速度大小(计算过程中100km/h近似为30m/s);
(2)若已知电动汽车电能转化为机械能的效率为η=80%,整车在行驶过程中的阻力约为车重的0.05倍,试估算此电动汽车以20m/s的速度匀速行驶时的续航里程(能够行驶的最大里程)已知1kWh=3.6×106J.根据你的计算,提出提高电动汽车的续航里程的合理化建议(至少两条)
(3)若此电动汽车的速度从5m/s提升到20m/s需要25s,此过程中电动汽车获得的动力功率随时间变化的关系简化如图所示,整车在行驶过程中的阻力仍约为车重的0.05倍,求此加速过程中汽车行驶的路程(提示:可利用p-t图像计算动力对电动汽车做的功)

查看答案和解析>>
科目: 来源: 题型:
【题目】在竖直平面内有一方向斜向上且与水平方向成α=30°角的匀强电场,电场中有一质量为m,电荷量为q的带电小球,用长为L的不可伸长的绝缘细线悬挂于O点,如图所示.开始时小球静止在M点,细线恰好水平.现用外力将小球拉到最低点P,然后由静止释放,则以下判断正确的是( )

A. 小球再次到M点时,速度刚好为零
B. 小球从P到M过程中,合外力对它做的功为![]()
C. 小球从P到M过程中,其机械能增加了![]()
D. 如果小球运动到M点时,细线突然断裂,小球将做匀变速直线运动
【答案】B
【解析】根据题述,开始时小球静止于M点,细线恰好水平,由平衡条件可知,![]() .小球再次到M点时,切向加速度为零,速度最大,选项A错误.小球从P到M过程中,重力做负功为WG=-mgL,电场力qE做正功为
.小球再次到M点时,切向加速度为零,速度最大,选项A错误.小球从P到M过程中,重力做负功为WG=-mgL,电场力qE做正功为![]() ,合外力对它做的功为
,合外力对它做的功为![]() ,选项B正确.由功能关系可知,电场力做功机械能增加,小球从P到M过程中,其机械能增加了
,选项B正确.由功能关系可知,电场力做功机械能增加,小球从P到M过程中,其机械能增加了![]() ,选项C错误.由于在M点,小球所受电场力在竖直方向的分量等于重力,如果小球运动到M点时,细线突然断裂,小球将做匀变速曲线运动,选项D错误.
,选项C错误.由于在M点,小球所受电场力在竖直方向的分量等于重力,如果小球运动到M点时,细线突然断裂,小球将做匀变速曲线运动,选项D错误.
【题型】单选题
【结束】
135
【题目】如图所示,一质量为m1的木箱放在水平地面上,一个质量为m2的人站在木箱里双手用力向上推木箱,推力为F,结果木箱和人仍静止不动,已知重力加速度为g,则( )
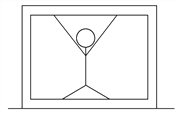
A. 人对木箱底部的压力大小为m2g
B. 人对木箱底部的压力大小为m2g+F
C. 木箱对地面的压力大小为m1g+m2g-F
D. 地面对木箱的支持力大小为m1g+m2g+F
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,有一半圆,其直径水平且与另一圆的底部相切于O点,O点恰好是下半圆的圆心,它们处在同一竖直平面内.现有三条光滑轨道AOB、COD、EOF,它们的两端分别位于上下两圆的圆周上,轨道与竖直直径的夹角关系为α>β>θ,现让一小物块先后从三条轨道顶端由静止下滑至底端,则小物块在每一条倾斜轨道上滑动时所经历的时间关系为( )

A. tAB=tCD=tEF
B. tAB>tCD>tEF
C. tAB<tCD<tEF
D. tAB=tCD<tEF
【答案】B
【解析】试题分析:设上面圆的半径为![]() ,下面圆的半径为
,下面圆的半径为![]() ,则轨道的长度
,则轨道的长度![]() ,下滑的加速度
,下滑的加速度![]() ,根据位移时间公式得,
,根据位移时间公式得,![]() ,则
,则![]() ,因为
,因为![]() ,则
,则![]() ,故B正确,A、C、D错误。
,故B正确,A、C、D错误。
考点:牛顿第二定律;匀变速直线运动的位移与时间的关系
【名师点睛】根据几何关系求出轨道的长度,结合牛顿第二定律求出物块下滑的加速度,根据位移时间公式求出物块在滑动时经历的时间大小关系。
【题型】单选题
【结束】
134
【题目】在竖直平面内有一方向斜向上且与水平方向成α=30°角的匀强电场,电场中有一质量为m,电荷量为q的带电小球,用长为L的不可伸长的绝缘细线悬挂于O点,如图所示.开始时小球静止在M点,细线恰好水平.现用外力将小球拉到最低点P,然后由静止释放,则以下判断正确的是( )

A. 小球再次到M点时,速度刚好为零
B. 小球从P到M过程中,合外力对它做的功为![]()
C. 小球从P到M过程中,其机械能增加了![]()
D. 如果小球运动到M点时,细线突然断裂,小球将做匀变速直线运动
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com