
(本题12分)△ABC中,∠A=∠B=30°,AB=![]() .把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.
.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.
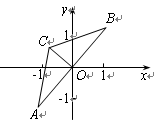
1.(1) 当点B在第一象限,纵坐标是![]() 时,求点B的横坐标;
时,求点B的横坐标;
2.(2) 如果抛物线![]() 的对称轴经过点C,请你探究:
的对称轴经过点C,请你探究:
①当![]() ,
,![]() ,
,![]() 时,A,B两点是否都在这条抛物线上?并说明理由;
时,A,B两点是否都在这条抛物线上?并说明理由;
②设 ![]() ,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
1.(1) ∵ 点O是AB的中点, ∴ ![]() . (1分)
. (1分)
设点B的横坐标是x(x>0),则![]() , (2分)
, (2分)
解得 ![]() ,
,![]() (舍去).
(舍去).
∴ 点B的横坐标是![]()
2.(2) ① 当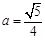 ,
,![]() ,
,![]() 时,得
时,得 ![]() (*)
(*)
![]() . (5分)
. (5分)
以下分两种情况讨论.
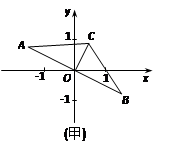 情况1:设点C在第一象限(如图甲),则点C的横坐标为
情况1:设点C在第一象限(如图甲),则点C的横坐标为![]() ,
,
![]() . (6分)
. (6分)
由此,可求得点C的坐标为(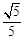 ,
,![]() ), (7分)
), (7分)
点A的坐标为(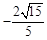 ,
,![]() ),
),
∵ A,B两点关于原点对称,
∴ 点B的坐标为 (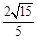 ,
,![]() ).
).
将点A的横坐标代入(*)式右边,计算得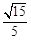 ,即等于点A的纵坐标;
,即等于点A的纵坐标;
将点B的横坐标代入(*)式右边,计算得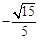 ,即等于点B的纵坐标.
,即等于点B的纵坐标.
∴ 在这种情况下,A,B两点都在抛物线上. (9分)
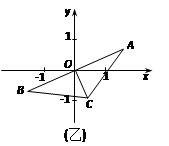 情况2:设点C在第四象限(如图乙),则点C的坐标为(
情况2:设点C在第四象限(如图乙),则点C的坐标为(![]() ,-
,-![]() ),
),
点A的坐标为(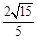 ,
,![]() ),点B的坐标为
),点B的坐标为
(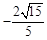 ,
,![]() ).
).
经计算,A,B两点都不在这条抛物线上. (10分)
② 存在.m的值是1或-1. (12分)
(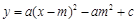 ,因为这条抛物线的对称轴经过点C,所以-1≤m≤1.当m=±1时,点C在x轴上,此时A,B两点都在y轴上.因此当m=±1时,A,B两点不可能同时在这条抛物线上)
,因为这条抛物线的对称轴经过点C,所以-1≤m≤1.当m=±1时,点C在x轴上,此时A,B两点都在y轴上.因此当m=±1时,A,B两点不可能同时在这条抛物线上)
解析:略


科目:初中数学 来源: 题型:
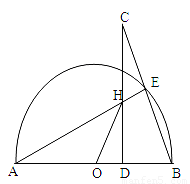
(本题12分)AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合。

1.(1)求证:△AHD∽△CBD
2.(2)若CD=AB=2,求HD+HO的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
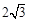 .把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.
.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.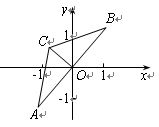
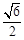 时,求点B的横坐标;
时,求点B的横坐标; 的对称轴经过点C,请你探究:
的对称轴经过点C,请你探究: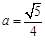 ,
,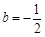 ,
,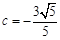 时,A,B两点是否都在这条抛物线上?并说明理由;
时,A,B两点是否都在这条抛物线上?并说明理由; ,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012年浙江省萧浦沿中学九年级12月月考数学卷 题型:解答题
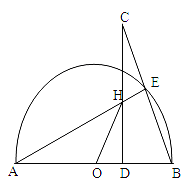
(本题12分)AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合。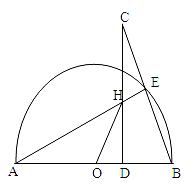
【小题1】(1)求证:△AHD∽△CBD
【小题2】(2)若CD=AB=2,求HD+HO的值。
查看答案和解析>>
科目:初中数学 来源:2011-2012年浙江省九年级12月月考数学卷 题型:解答题
(本题12分)AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合。
1.(1)求证:△AHD∽△CBD
2.(2)若CD=AB=2,求HD+HO的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com