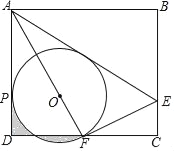
【题目】如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB＝6，BC＝3，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE＝CE；④S阴影＝．其中正确的个数为（　　）

A. 1 B. 2 C. 3 D. 4

A.45°B.60°C.70°D.90°

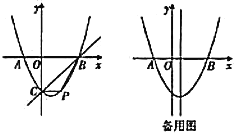
【题目】如图，抛物线的顶点坐标为，点的坐标为，为直线下方抛物线上一点，连接，．

（1）求抛物线的解析式．

（2）的面积是否有最大值？如果有，请求出最大值和此时点的坐标；如果没有，请说明理由．

（3）为轴右侧抛物线上一点，为对称轴上一点，若是以点为直角顶点的等腰直角三角形，请直接写出点的坐标．

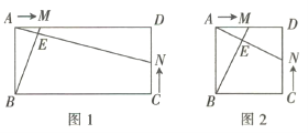
【题目】如图1，在矩形中，，点从点出发向点移动，速度为每秒1个单位长度，点从点出发向点移动，速度为每秒2个单位长度. 两点同时出发，且其中的任何一点到达终点后，另一点的移动同时停止.

（1）若两点的运动时间为，当为何值时，？

（2）在（1）的情况下，猜想与的位置关系并证明你的结论.

（3）①如图2，当时，其他条件不变，若（2）中的结论仍成立，则_________.

②当，时，其他条件不变，若（2）中的结论仍成立，则_________（用含的代数式表示）.

【题目】某农科所研究出一种新型的花生摘果设备，一期研发成本为每台6万元，该摘果机的销售量(台)与售价(万元/台)之间存在函数关系：．

（1）设这种摘果机一期销售的利润为(万元)，问一期销售时，在抢占市场份额(提示：销量尽可能大)的前提下利润达到32万元，此时售价为多少？

（2）由于环保局要求该机器必须增加除尘设备，科研所投入了7万元研究经费，使得环保达标且机器的研发成本每台降低了1万元，若科研所的销售战略保持不变，请问在二期销售中利润达到63万元时，该机器单台的售价为多少？

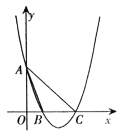
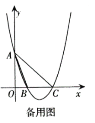
【题目】如图，抛物线交轴于，两点，交轴于点，连接，点为抛物线上一动点．

（1）求抛物线的解析式；

（2）当点到直线的距离为时，求点的横坐标；

（3）当和的面积相等时，请直接写出点的坐标．

【题目】如图1，在中，，，点分别在边上，，连接、，点为的中点．

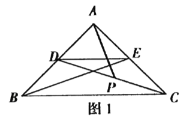
（1）观察猜想

图1中，线段与的数量关系是______，位置关系是________；

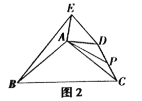
（2）探究证明

把绕点逆时针方向旋转到图2的位置，小航猜想（1）中的结论仍然成立，请你证明小航的猜想；

（3）拓展延伸

把绕点在平面内自由旋转，若，，请直接写出线段的取值范围．

【题目】某公司推出一款产品，成本价10元/千克，经过市场调查，该产品的日销售量（千克）与销售单价（元/克）之间满足一次函数关系，该产品的日销售量与销售单价之间的几组对应值如下表：

（注：日销售利润=日销售量×（销售单价-成本单价））

（1）求关于的函数解析式（不要求写出的取值范围）；

（2）根据以上信息，填空：

①_____元；

②当销售价格_____元时，日销售利润最大，最大值是______元；

（3）该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象，为了保证捐赠后每天的剩余利润不低于1025元，试确定该产品销售单价的范围．

【题目】某学校为增加体育馆观众坐席数量，决定对体育馆进行施工改造．如图，为体育馆改造的截面示意图．已知原座位区最高点A到地面的铅直高度AC长度为15米，原坡面AB的倾斜角∠ABC为45°，原坡脚B与场馆中央的运动区边界的安全距离BD为5米．如果按照施工方提供的设计方案施工，新座位区最高点E到地面的铅直高度EG长度保持15米不变，使A、E两点间距离为2米，使改造后坡面EF的倾斜角∠EFG为37°．若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米（即FD≥2.5），请问施工方提供的设计方案是否满足安全要求呢？请说明理由．（参考数据：sin37°≈，tan37°≈）