
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
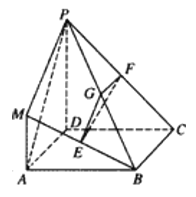
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之比.
的体积之比.
【答案】(1)(2)证明过程详见解析;(3)1:4
【解析】试题分析:(1)欲证平面![]() 平面
平面![]() ,根据面面垂直的判定定理可知在平面
,根据面面垂直的判定定理可知在平面![]() 内一直线与平面
内一直线与平面![]() 垂直,而根据线面垂直的判定定理可知
垂直,而根据线面垂直的判定定理可知![]() 平面
平面![]() 平面
平面![]() ,满足定理条件;(2)证明
,满足定理条件;(2)证明![]() ,利用线面平行的判定定理,即可证明
,利用线面平行的判定定理,即可证明![]() 平面
平面![]() ;(3)不妨设
;(3)不妨设![]() ,求出
,求出![]() ,得到
,得到![]() ,求出PD,根据
,求出PD,根据![]() 面
面![]() ,所以
,所以![]() 即为点
即为点![]() 到平面
到平面![]() 的距离,根据三棱锥的体积公式求出体积得到
的距离,根据三棱锥的体积公式求出体积得到![]() 的比值.
的比值.
试题解析:
(1)证明:∵![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,
,
又∵四边形![]() 是正方形,
是正方形,
∴![]() ,∴
,∴![]() ,
,
∵![]() 在平面
在平面![]() 外,
外, ![]() 在平面
在平面![]() 内,
内,
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
又∵![]() 都在平面
都在平面![]() 内且相交,
内且相交,
∴平面![]() 平面
平面![]() .
.
(2)证明:由已知![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() .
.
∵四边形![]() 为正方形,∴
为正方形,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
在![]() 中,∵
中,∵![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(3)解:∵![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,不妨设
为正方形,不妨设![]() ,则
,则![]() .
.
∵![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 即为点
即为点![]() 到平面
到平面![]() 的距离,
的距离,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l: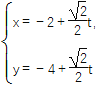 (t为参数)与曲线C相交于M,N两点.
(t为参数)与曲线C相交于M,N两点.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 也是抛物线
也是抛物线![]() 的焦点,点M为
的焦点,点M为![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)平面上的点N满足![]() ,直线
,直线![]() ,且与
,且与![]() 交于A,B两点,若
交于A,B两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c.已知c=2,C=![]() .
.
(1)若△ABC的面积等于![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区工商局、消费者协会在![]() 月
月![]() 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取![]() 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
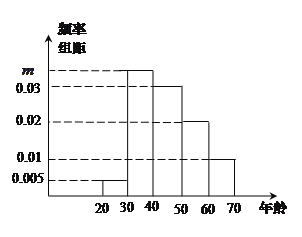
(Ⅰ)若电视台记者要从抽取的群众中选![]() 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第![]() 组或第
组或第![]() 组的概率;
组的概率;
(Ⅱ)已知第![]() 组群众中男性有
组群众中男性有![]() 人,组织方要从第
人,组织方要从第![]() 组中随机抽取
组中随机抽取![]() 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosφ,sinφ)(|φ|<
=(cosφ,sinφ)(|φ|<![]() ).函数
).函数
f(x)=![]()
![]() 且f(
且f(![]() -x)=f(x).
-x)=f(x).
(Ⅰ)求f(x)的解析式及单调递增区间;
(Ⅱ)将f(x)的图象向右平移![]() 单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0,
单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0, ![]() ]上恒成立,求实数a的取值范围.
]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),当
为参数),当![]() 时,曲线
时,曲线![]() 上对应的点为
上对应的点为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设曲线![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com