
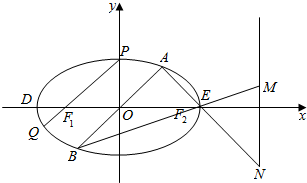
分析 (Ⅰ)①运用离心率公式和a,b,c的关系,可得a,b,进而得到椭圆方程;
②设直线AB:y=kx,代入椭圆方程,求得A,B的坐标,再由三点共线的知识:斜率相等,可得M,N的坐标,设T(t,0),运用向量的数量积的坐标表示,解方程可得T的坐标;
(Ⅱ)设AB:y=$\frac{b}{c}$x,代入椭圆方程,求得A,B的坐标,求得AB的距离,再由由PQ的方程:y=$\frac{b}{c}$x+b,代入椭圆方程,求得Q的坐标,求得PQ的距离,再由条件,可得a,c的方程,运用离心率公式计算即可得到所求值.
解答 解:(Ⅰ)①由题意可得c=1,e=$\frac{c}{a}$=$\frac{1}{2}$,
可得a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
即有椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
②设直线AB:y=kx,代入椭圆方程可得,x=±$\sqrt{\frac{12}{3+4{k}^{2}}}$,
即有A($\frac{2\sqrt{3}}{\sqrt{3+4{k}^{2}}}$,$\frac{2\sqrt{3}k}{\sqrt{3+4{k}^{2}}}$),B(-$\frac{2\sqrt{3}}{\sqrt{3+4{k}^{2}}}$,-$\frac{2\sqrt{3}k}{\sqrt{3+4{k}^{2}}}$),
椭圆的右准线方程为x=4,设M(4,y1),N(4,y2),
又E(2,0),由A,E,N共线,可得kAE=kNE,
即$\frac{2\sqrt{3}k}{2\sqrt{3}-2\sqrt{3+4{k}^{2}}}$=$\frac{{y}_{2}}{2}$,解得y2=$\frac{2\sqrt{3}k}{\sqrt{3}-\sqrt{3+4{k}^{2}}}$,
同理由B,E,M共线,可得y1=$\frac{2\sqrt{3}k}{\sqrt{3}+\sqrt{3+4{k}^{2}}}$,
在x轴上假设存在定点T,使TM⊥TN.
设T(t,0),$\overrightarrow{TM}$•$\overrightarrow{TN}$=(4-t)2+y1y2═(4-t)2+$\frac{12{k}^{2}}{3-3-4{k}^{2}}$=0,
解得t=4±$\sqrt{3}$,
则在x轴上存在定点T(4±$\sqrt{3}$,0),使TM⊥TN.
(Ⅱ)若直线PF1∥AB,即有kAB=$\frac{b}{c}$,
设AB:y=$\frac{b}{c}$x,代入椭圆方程b2x2+a2y2=a2b2,可得,
x=±$\frac{ac}{\sqrt{{a}^{2}+{c}^{2}}}$,即有A($\frac{ac}{\sqrt{{a}^{2}+{c}^{2}}}$,$\frac{ab}{\sqrt{{a}^{2}+{c}^{2}}}$),B(-$\frac{ac}{\sqrt{{a}^{2}+{c}^{2}}}$,-$\frac{ab}{\sqrt{{a}^{2}+{c}^{2}}}$),
则|AB|=$\frac{2{a}^{2}}{\sqrt{{a}^{2}+{c}^{2}}}$;
由PQ的方程:y=$\frac{b}{c}$x+b,代入椭圆方程,可得x=-$\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$,
即有Q(-$\frac{2{a}^{2}c}{{a}^{2}+{c}^{2}}$,$\frac{b({c}^{2}-{a}^{2})}{{c}^{2}+{a}^{2}}$),又P(0,b),
可得|PQ|=$\frac{2{a}^{3}}{{a}^{2}+{c}^{2}}$,
由$\frac{AB}{PQ}=\frac{\sqrt{5}}{2}$,可得2$\sqrt{{a}^{2}+{c}^{2}}$=$\sqrt{5}$a,
化简可得a=2c,即有离心率e=$\frac{c}{a}$=$\frac{1}{2}$.
点评 本题考查椭圆的方程和性质,考查直线和椭圆方程联立,求得交点,考查向量的数量积的坐标表示和直线方程的运用,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | [0,π2) | C. | $[0\;,\;\frac{π^2}{4})$ | D. | [0,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
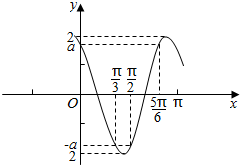 已知函数f(x)=Asin(ωx+φ).
已知函数f(x)=Asin(ωx+φ).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com