
已知奇函数f(x)=
(1)求实数m的值,并在给出的直角坐标系中画出y=f(x)的图象;
(2)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围.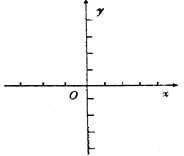
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)
某公司生产一种电了仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: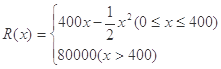 ,其中
,其中 是仪器的月产量。
是仪器的月产量。
⑴将利润表示为月产量的函数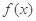 。
。
⑵当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益―总成本=利润)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.(12分)飞机每飞行1小时的费用由两部分组成,固定部分为4900元,变动部分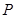 (元)与飞机飞行速度
(元)与飞机飞行速度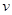 (千米∕小时)的函数关系式是
(千米∕小时)的函数关系式是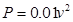 ,已知甲乙两地的距离为
,已知甲乙两地的距离为 (千米).
(千米).
(1)试写出飞机从甲地飞到乙地的总费用 (元)关于速度
(元)关于速度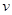 (千米∕小时)的函数关系式;
(千米∕小时)的函数关系式;
(2)当飞机飞行速度为多少时,所需费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地有三家工厂,分别位于矩形ABCD 的顶点A,B 及CD的中点P 处,已知AB="20km,CB" ="10km" ,为了处理三家工厂的污水,现要在矩形ABCD 的区域中(含边界),且与A,B等距离的一点O 处建造一个污水处理厂,并铺设排污管道AO,BO,OP ,设排污管道的总长为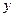 km.
km.
(Ⅰ)设∠BAO=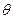 (rad),将
(rad),将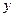 表示成
表示成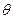 的函数关系式;
的函数关系式;
(Ⅱ)请用(Ⅰ)中的函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短.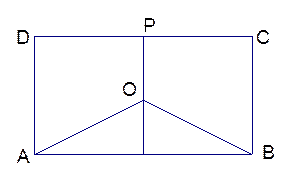
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某出版社新出版一本高考复习用书,该书的成本为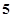 元一本,经销过程中每本书需付给代理商
元一本,经销过程中每本书需付给代理商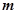 元
元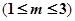 的劳务费,经出版社研究决定,新书投放市场后定价为
的劳务费,经出版社研究决定,新书投放市场后定价为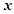 元一本,
元一本,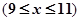 ,预计一年的销售量为
,预计一年的销售量为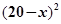 万本.
万本.
(Ⅰ)求该出版社一年的利润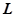 (万元)与每本书的定价
(万元)与每本书的定价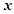 的函数关系式;
的函数关系式;
(Ⅱ)若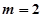 时,当每本书的定价为多少元时,该出版社一年利润
时,当每本书的定价为多少元时,该出版社一年利润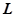 最大,并求出
最大,并求出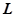 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com