Question

(理)对任意实数x、y,函数f(x)、g(x)满足f(x+1)=f(x),且f(0)=3,g(x+y)=g(x)+2y,g(5)=13,n∈N^*.

(1)求{f(n)}、{g(n)}的通项公式;

(2)设c_n=g［f(n)］,求数列{c_n}的前n项和;

(3)已知=0,设F(n)=S_n-3n,是否存在整数m和M,使得对任意正整数n,不等式m＜F(n)＜M恒成立?若存在,分别求出m和M的集合,并求出M-m的最小值;若不存在,请说明理由.

(文)已知f(x)=x³-3x,g(x)=2ax².

(1)当-≤a≤时,求证:F(x)=f(x)-g(x)在(-1,1)上是单调函数;

(2)若g′(x)≤〔g′(x)为g(x)的导函数〕在［-1,］上恒成立,求a的取值范围.

Answer 1

答案：(理)解:(1)取x=n,则f(n+1)=f(n).取x=0,得f(1)=f(0)=1.

故{f(n)}是首项为1,公比为的等比数列.∴f(n)=()^n-1.

取x=n,y=1,得g(n+1)=g(n)+2(n∈N^*),即g(n+1)-g(n)=2.

∴g(n)是公差为2的等差数列.又g(5)=13,因此g(n)=13+2(n-5)=2n+3,即g(n)=2n+3.

(2)∵c_n=g[f(n)]=g[()^n-1]=n()^n-1+3,∴S_n=c₁+c₂+…+c_n=1+2×()+3×()²+…+(n-1)()^n-2+n()^n-1+3n,S_n=+2×()²+…+(n-1)()^n-1+n()ⁿ+n.

两式相减,得S_n=1++()²+…+()^n-1-n()ⁿ+2n=-n()ⁿ+2n,

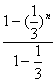S_n=[1-()ⁿ]-()ⁿ+3n=-()^n-1-()^n-1+3n=.

(3)∵F(n)=S_n-3n=·()^n-1,∴F(n+1)-F(n)=.

∴F(n)为增函数.故F(n)_min=F(1)=1.∵=0,∴F(n)=.又·()^n-1＞0,F(n)＜,∴1≤F(n)＜.因此,当m＜1,且M≥时m＜F(n)＜M恒成立.

∴存在整数m=0,-1,-2,-3,…,M=3,4,5,6,…,使得对任意正整数n,不等式m＜F(n)＜M恒成立.

此时,m的集合是{0,-1,-2,-3,…},M的集合是{3,4,5,6,…},且(M-m)_min=3.

(文)(1)证明:∵F(x)=x³-3x-2ax²,∴F′(x)=2x²-4ax-3=2(x-a)²-2a²-3,F′(1)=-4a-1,F′(-1)=4a-1.

又∵-≤a≤,∴F′(-1)≤0,F′(1)≤0.导函数F′(x)在[-1,1]上的最大值为F′(1)或F′(-1),F′(x)在(-1,1)上总有F′(x)＜0,故F(x)=x³-3x-2ax²在(-1,1)上单调递减.

(2)解:g′(x)=4ax.

①当x=0时,不等式g′(x)≤显然成立.

②当-1≤x＜0时,不等式4ax≤可化为a≥.

而u(x)=(-1≤x＜0)的最大值为-,∴a≥-.

③当0＜x≤时,不等式4ax≤可化为a≤.

而当0＜x≤时,x(1-x)的最大值为,u(x)=(0＜x≤)的最小值为1.故a满足条件的取值范围是(-∞,1].综上所述,得-≤a≤1.