
分析 (Ⅰ)把a1,a3,a4,a2,a5分别代入E(a1,a2,…,an)=|a1-1|+|a2-2|+…+|an-n|进行解答即可;
(Ⅱ)分两种情况进行讨论:当ai=i+1,ai+1=i,aj=j+1,aj+1=j,且{ai,ai+1}∩{aj,aj+1}=∅,其他项ak=k(其中k∉{i,i+1,j,j+1})时和当ai,ai+1,ai+2分别等于i+2,i+1,i或i+1,i+2,i或i+2,i+1,其他项ak=k(其中k∉{i,i+1,i+2});
(Ⅲ)此题实际上求位差和E(a1,a2,…,an)最大值为$\frac{{{n^2}-1}}{2}$,且给出取得最大值时,数列{an}:a1,a2,…,an的情况.
解答 解:(I)E(1,3,4,2,5)=|1-1|+|3-2|+|4-3|+|2-4|+|5-5|=4;
(II)若数列{an}:a1,a2,…,an的位差和E(a1,a2,…,an)=4,有如下两种情况:
情况一:当ai=i+1,ai+1=i,aj=j+1,aj+1=j,且{ai,ai+1}∩{aj,aj+1}=∅,其他项ak=k(其中k∉{i,i+1,j,j+1})时,有$({n-3})+({n-4})+…+2+1=\frac{{({n-2})({n-3})}}{2}$种可能;
情况二:当ai,ai+1,ai+2分别等于i+2,i+1,i或i+1,i+2,i或i+2,i+1,其他项ak=k(其中k∉{i,i+1,i+2})时,有3(n-2)种可能;
综上,满足条件的数列{an}:a1,a2,…,an的个数为$\frac{{({n-2})({n-3})}}{2}+3({n-2})=\frac{{({n-2})({n+3})}}{2}$.
例如:n=5时,
情况一:形如2,1,4,3,5,共有2+1=3种:2,1,4,3,5;2,1,3,5,4;1,3,2,5,4;
情况二:形如3,2,1,4,5,共有5-2=3种:3,2,1,4,5;1,4,3,2,5;1,2,5,4,3;
形如2,3,1,4,5,共有5-2=3种:2,3,1,4,5;1,3,4,2,5;1,2,4,5,3;
形如3,1,2,4,5,共有5-2=3种:3,1,2,4,5;1,4,2,3,5;1,2,5,3,4.
(III)将|a1-1|+|a2-2|+…+|an-n|去绝对值符号后,所得结果为±1±1±2±2±3±3±…±n±n
的形式,其中恰好有n个数前面为减号,这表明:
$E({{a_1},\;\;{a_2},\;…,\;\;{a_n}})=\sum_{i=1}^n{|{a_i}-i|}$$≤2({n+({n-1})+…+\frac{n+3}{2}})+\frac{n+1}{2}-\frac{n+1}{2}-2({\frac{n-1}{2}+…+2+1})$
=$2({({n-\frac{n-1}{2}})+({n-1-\frac{n-3}{2}})+…+({\frac{n+3}{2}-1})})\frac$,
=$\frac{{{n^2}-1}}{2}$.
此不等式成立是因为前面为减号的n个数最小为:2个1,2个2,…,2个$\frac{n-1}{2}$和1个$\frac{n+1}{2}$.
上面的讨论表明,题中所求的数列{an}:a1,a2,…,an是使得E(a1,a2,…,an)最大的数列,这样的数列在n=2k+1时,要求从1,2,…,n中任选一个数作为
ak+1,将剩余数中较大的k个数的排列作为a1,a2,…,ak的对应值,较小的k个数的排列作为ak+2,ak+3,…,a2k+1的对应值,
于是所求数列的个数为(2k+1)(k!)2.
综上,满足条件的数列的个数为$n{({({\frac{n-1}{2}})!})^2}$
例如:n=5时,
E(a1,a2,a3,a4,a5)=$\sum_{i=1}^5{|{a_i}-i|}$.≤2(5+4)+3-3+2(2+1)=2[(5-2)+(4-1)]=$2•\underbrace{({5-\frac{5-1}{2}})}_{每组之差}•\underbrace{({\frac{5-1}{2}})}_{组数}$=$2({\frac{5+1}{2}})({\frac{5-1}{2}})$=$\frac{{{5^2}-1}}{2}=12$
此不等式成立是因为前面为减号的5个数最小为:2个1,2个2和1个3.
若E(a1,a2,a3,a4,a5)=12,n=2k+1=5,此时k=2时,要求从1,2,3,4,5中任选一个数作为a3,将剩余数中较大的2个数的排列作为a1,a2的对应值,
较小的2个数的排列作为a4,a5的对应值,于是所求数列的个数为5•(2!)2=20.
4,5,1,2,3;4,5,1,3,2;5,4,1,2,3;5,4,1,3,2;
4,5,2,1,3;4,5,2,3,1;5,4,2,1,3;5,4,2,3,1;
4,5,3,1,2;4,5,3,2,1;5,4,3,1,2;5,4,3,2,1;
3,5,4,1,2;3,5,4,2,1;5,3,4,1,2;5,3,4,2,1;
3,4,5,1,2;3,4,5,2,1;4,3,5,1,2;4,3,5,2,1.
点评 本题考查了数列的应用.假设现在有n种物品,已经按照某种标准排列,并依次确定编号为1,2,…,n,鉴别师事先不知道物品的标准排列编号,而是根据自己的判断,对这n种物品进行排列依次编号为a1,a2,…,an,其中a1,a2,…,an是1,2,…,n的一个排列,那么可以用数列{an}:a1,a2,…,an的位差和E(a1,a2,…,an)=|a1-1|+|a2-2|+…+|an-n|,来评判鉴别师的能力.
当E(a1,a2,…,an)越小,说明鉴别师能力越强;反之越大,说明鉴别师能力越弱;
当E(a1,a2,…,an)=0,说明鉴别师给出的排列编号与标准排列编号一致,判断完全正确;
第二问,位差和E(a1,a2,…,an)=4时,给出数列{an}:a1,a2,…,an的情况;
第三问,说明位差和E(a1,a2,…,an)最大值为$\frac{{{n^2}-1}}{2}$,且给出取得最大值时,数列{an}:a1,a2,…,an的情况.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
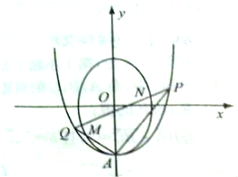 如图,过抛物线C1:y=$\frac{1}{4}$x2-2的顶点A作两条斜率之积为-$\frac{1}{4}$的直线,与抛物线交于另两点P、Q直线(PQ不与x轴垂直)与椭圆C2:$\frac{{y}^{2}}{4}$+x2=1相交于点M、N.
如图,过抛物线C1:y=$\frac{1}{4}$x2-2的顶点A作两条斜率之积为-$\frac{1}{4}$的直线,与抛物线交于另两点P、Q直线(PQ不与x轴垂直)与椭圆C2:$\frac{{y}^{2}}{4}$+x2=1相交于点M、N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | 2+i | D. | 2-i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com