【题目】如图，在正方体ABCD－ABCD中,平面
垂直于对角线AC,且平面截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则（ ）
A. S为定值,l不为定值 B. S不为定值,l为定值
C. S与l均为定值 D. S与l均不为定值
【答案】B
【解析】
将正方体切去两个正三棱锥
和
，得到一个几何体
，是以平行平面
和
为上下底，每个侧面都是直角等腰三角形，截面多边形的每一条边分别与的底面上的一条边平行，设正方体棱长为
，
，可求得六边形的周长为
与
无关，即周长为定值；当
都在对应棱的中点时，
是正六边形，计算可得面积
，当无限趋近于时，的面积无限趋近于
，从而可知的面积一定会发生变化。
设平面
截得正方体的六个表面得到截面六边形为，与正方体的棱的交点分别为（如下图），
将正方体切去两个正三棱锥和，得到一个几何体，是以平行平面和为上下底，每个侧面都是直角等腰三角形，截面多边形的每一条边分别与的底面上的一条边平行，设正方体棱长为，，则
，
，故
，同理可证明
，故六边形的周长为，即周长为定值；
当都在对应棱的中点时，是正六边形，计算可得面积
，三角形的面积为
，当无限趋近于时，的面积无限趋近于，故的面积一定会发生变化，不为定值。
故答案为B.
科目：高中数学 来源： 题型：
【题目】若对满足条件3x+3y+8＝2xy（x＞0，y＞0）的任意x、y，（x+y）2﹣a（x+y）+16≥0恒成立，则实数a的取值范围是（ ）
A.（﹣∞，8]B.[8，+∞）C.（﹣∞，10]D.[10，+∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知五边形ABECD由一个直角梯形ABCD与一个等边三角形BCE构成，如图1所示,AB丄BC，AB//CD，且AB=2CD。将梯形ABCD沿着BC折起，如图2所示，且AB丄平面BEC。
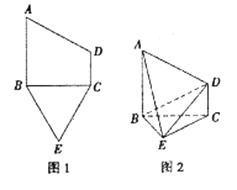
(1)求证:平面ABE丄平面ADE；
(2)若AB=BC,求二面角A-DE-B的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有一块半径为
，圆心角为
的扇形钢板，需要将它截成一块矩形钢板，分别按图1和图2两种方案截取（其中方案二中的矩形关于扇形的对称轴对称）．
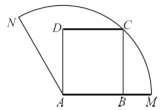
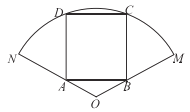
图1：方案一 图2：方案二
（1）求按照方案一截得的矩形钢板面积的最大值；
（2）若方案二中截得的矩形
为正方形，求此正方形的面积；
（3）若要使截得的钢板面积尽可能大，应选择方案一还是方案二？请说明理由，并求矩形钢板面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
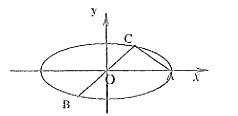
【题目】如图已知椭圆
，
是长轴的一个端点，弦
过椭圆的中心
，且
，
.
（Ⅰ）求椭圆的方程：
（Ⅱ）设
为椭圆上异于
且不重合的两点，且
的平分线总是垂直于
轴，是否存在实数
，使得
，若存在，请求出的最大值，若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设点
，
分别是椭园C：
的左、右焦点，且椭圆C上的点到的距离的最小值为
，点M，N是椭圆C上位于x轴上方的两点，且向量
与向量
平行．
求椭圆C的方程；
当
时，求
的面积；
当
时，求直线
的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某些竞赛活动中，选手的最终成绩是将前面所有轮次比赛成绩求算术平均获得的.同学们知道这样一个事实：在所有轮次的成绩中，如果由高到低依次去掉一些高分，那么平均分降低；反之，如果由低到高依次去掉一些低分，那么平均分提高. 这两个事实可以用数学语言描述为：若有限数列
满足
，且
不全相等，则(1)_______；(2)_______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
