Question

【题目】已知F1 ， F2分别是椭圆 的左、右焦点F1 ， F2关于直线x+y﹣2=0的对称点是圆C的一条直径的两个端点．
（1）求圆C的方程；
（2）设过点F2的直线l被椭圆E和圆C所截得的弦长分别为a，b．当ab最大时，求直线l的方程．

Answer 1

【答案】
（1）解：由题意可知：F1（﹣2，0），F2（2，0）．故⊙C的半径为2，圆心为原点O关于直线x+y﹣2=0的对称点．设圆心的坐标为（m，n）．则 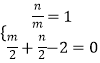，解得 ．

∴圆C的方程为（x﹣2）2+（y﹣2）2=4；

（2）解：由题意，可设直线l的方程为x=my+2，则圆心到直线l的距离d= ，

∴b= ．

由 得（5+m2）y2+4my﹣1=0．

设l与E的两个交点分别为（x1，y1），（x2，y2）．

则 ， ．

∴a= = = ，

∴ab= = = ．

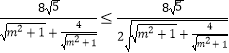当且仅当 ，即 时等号成立．

故当 时，ab最大，此时，直线l的方程为 ，即 ．

【解析】（1）由题意可知：F1（﹣2，0），F2（2，0），可得⊙C的半径为2，圆心为原点O关于直线x+y﹣2=0的对称点．设圆心的坐标为（m，n）．利用线段的垂直平行的性质可得 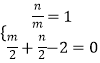，解出即可得到圆的方程；（2））由题意，可设直线l的方程为x=my+2，利用点到直线的距离公式可得圆心到直线l的距离d= ，再利用弦长公式即可得到b= ．把直线l的方程为x=my+2与椭圆的方程联立得到根与系数的关系，利用弦长公式即可得到a，进而得到ab，利用基本不等式的性质即可得出结论．
【考点精析】本题主要考查了圆的标准方程的相关知识点，需要掌握圆的标准方程：；圆心为A(a,b),半径为r的圆的方程才能正确解答此题．