
【题目】已知 ![]() ,且cos(α﹣β)=
,且cos(α﹣β)= ![]() ,sin(α+β)=﹣
,sin(α+β)=﹣ ![]() ,求:cos2α的值.
,求:cos2α的值.
【答案】解:∵ ![]() <β<α<
<β<α< ![]() ,∴0<α﹣β<
,∴0<α﹣β< ![]() ,π<α+β<
,π<α+β< ![]() ,
,
∵cos(α﹣β)= ![]() ,sin(α+β)=﹣
,sin(α+β)=﹣ ![]() ,
,
∴sin(α﹣β)=  =
= ![]() ,cos(α+β)=﹣
,cos(α+β)=﹣  =﹣
=﹣ ![]() ,
,
则cos2α=cos[(α﹣β)+(α+β)]=cos(α﹣β)cos(α+β)﹣sin(α﹣β)sin(α+β)= ![]() ×(﹣
×(﹣ ![]() )﹣(﹣
)﹣(﹣ ![]() )×
)× ![]() =﹣
=﹣ ![]() .
.
【解析】由α与β的范围求出α﹣β与α+β的范围,利用同角三角函数间的基本关系求出sin(α﹣β)与cos(α+β)的值,所求式子角度变形后利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
【考点精析】本题主要考查了两角和与差的余弦公式和二倍角的余弦公式的相关知识点,需要掌握两角和与差的余弦公式:![]() ;二倍角的余弦公式:
;二倍角的余弦公式:![]() 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
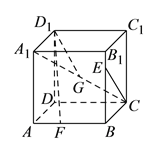
【题目】已知正方体![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 和
和![]() 上的动点,观察直线
上的动点,观察直线![]() 与
与![]() ,
, ![]() 与
与![]() .给出下列结论:
.给出下列结论:
①对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
②对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
③对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
④对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() .
.
其中正确结论的个数是( ).
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知内角 ![]() ,边
,边 ![]() .设内角B=x,△ABC的面积为y.
.设内角B=x,△ABC的面积为y.
(1)求函数y=f(x)的解析式和定义域;
(2)当角B为何值时,△ABC的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 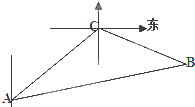
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]()
![]() ,说明满足条件的点
,说明满足条件的点![]() 的轨迹,并求
的轨迹,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com