
【题目】癌症是迄今为止人类尚未攻克的疾病之一,目前,癌症只能尽量预防.某医学中心推出了一种抗癌症的制剂,现对20位癌症病人,进行医学试验测试药效,测试结果分为“病人死亡”和“病人存活”,现对测试结果和药物剂量(单位:![]() )进行统计,规定病人在服用
)进行统计,规定病人在服用![]() (包括
(包括![]() )以上为“足量”,否则为“不足量”,统计结果显示,这20病人
)以上为“足量”,否则为“不足量”,统计结果显示,这20病人
中“病人存活”的有13位,对病人服用的药物剂量统计如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量/ | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
已知“病人存活”,但服用的药物剂量不足的病人共1位.
(1)完成下列![]() 列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为“病人存活”与服用药物的剂量足量有关?
列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为“病人存活”与服用药物的剂量足量有关?
服用药物足量 | 服用药物不足量 | 合计 | |
病人存活 | 1 | ||
病人死亡 | |||
合计 | 20 |
(2)若在该样本“服用药物剂量不足”的病人中随机抽取3位,求这三人中恰有1位“病人存活”的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
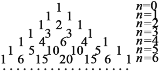
基于上述规律,可以推测,当![]() 时,从左往右第22个数为_____________.
时,从左往右第22个数为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在A,B实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在A,B试验地随机抽选各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.

(1)求图中a的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,若在A,B两块实验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望;
(3)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,PA⊥平面ABC,AC⊥BC,D为PC中点,E为AD中点,PA=AC=2,BC=1.

(1)求证:AD⊥平面PBC:
(2)求PE与平面ABD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD所在平面与直角梯形ABEF所在平面互相垂直,且![]() ,
,![]() ,P为DF中点.
,P为DF中点.

(1)求证:直线PE平行于平面ABCD;
(2)求PE与平面BCE所成的线面角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为
与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为![]() .
.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB分别表示直线MA,MB的斜率,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:

将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有10名女生.
类学生中有10名女生.
(1)根据已知条件完成下面![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为达到体育健康
的把握认为达到体育健康![]() 类学生与性别有关?
类学生与性别有关?
非体育健康 | 体育健康 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为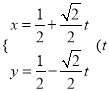 为参数), 椭圆C的参数方程为
为参数), 椭圆C的参数方程为![]() 为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2,
为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2, ![]()
(1)求椭圆C的直角坐标方程和点A在直角坐标系下的坐标
(2)直线l与椭圆C交于P,Q两点,求△APQ的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com