
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求证:
时,求证:![]() 在
在![]() 上有唯一零点.
上有唯一零点.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在A,B实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在A,B试验地随机抽选各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.

(1)求图中a的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,若在A,B两块实验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望;
(3)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为
与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为![]() .
.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB分别表示直线MA,MB的斜率,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:
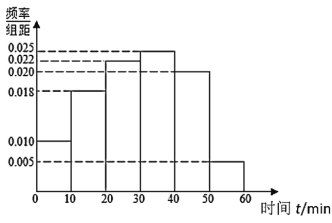
将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有10名女生.
类学生中有10名女生.
(1)根据已知条件完成下面![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为达到体育健康
的把握认为达到体育健康![]() 类学生与性别有关?
类学生与性别有关?
非体育健康 | 体育健康 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意程度进行调查,并随机抽取了其中30名员工(16名女工,14名男工)的得分,如下表:
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平局得分为 “满意”,否则为 “不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女员工 | 16 | ||
男员工 | 14 | ||
合计 | 30 |
(3)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
P(K2 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为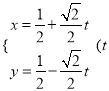 为参数), 椭圆C的参数方程为
为参数), 椭圆C的参数方程为![]() 为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2,
为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2, ![]()
(1)求椭圆C的直角坐标方程和点A在直角坐标系下的坐标
(2)直线l与椭圆C交于P,Q两点,求△APQ的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的![]() ,都有
,都有![]() ;②对于任意的
;②对于任意的![]() 都有
都有![]() ③函数
③函数![]() 的图象关于y轴对称,则下列结论中正确的是( )
的图象关于y轴对称,则下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com