
分析 由斜率公式得y1-y2=k(x1-x2),由此利用完全平方式能证明|P1P2|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$.
解答 证明:∵P1(x1,y1),P2(x2,y2)是斜率为k的直线上的两点,
∴$k=\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$,∴y1-y2=k(x1-x2),
∴|P1P2|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
=$\sqrt{({x}_{1}-{x}_{2})^{2}+[k({x}_{1}-{x}_{2})]^{2}}$
=$\sqrt{(1+{k}^{2})({x}_{1}-{x}_{2})^{2}}$
=$\sqrt{1+{k}^{2}}•|{x}_{1}-{x}_{2}|$
=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$.
∴|P1P2|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$.
点评 本题考查两点间距离公式的证明,是基础题,解题时要注意直线斜率公式和完全平方式的合理运用.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120°角与420°角的终边相同 | |
| B. | 若α是锐角.则2α是第二象限的角 | |
| C. | -240°角与480°角都是第三象限的角 | |
| D. | 60°角与-420°角的终边关于x轴对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
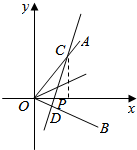 如图,射线OA,OB与x轴的正方向分别成45°与30°的角,过点P(1,0)的直线与两射线分别交于C,D,若线段CD的中点恰好在直线y=$\frac{1}{2}$x上,求CD所在直线的方程.
如图,射线OA,OB与x轴的正方向分别成45°与30°的角,过点P(1,0)的直线与两射线分别交于C,D,若线段CD的中点恰好在直线y=$\frac{1}{2}$x上,求CD所在直线的方程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±2 | C. | 2$\sqrt{3}$ | D. | ±2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com