已知函数f(x)=x3+3ax-1的导函数为f′(x),g(x)=f′(x)-ax-3.
(1)当a=-2时,求函数f(x)的单调区间;
(2)若对满足-1≤a≤1的一切a的值,都有g(x)<0,求实数x的取值范围;
(3)若x•g′(x)+lnx>0对一切x≥2恒成立,求实数a的取值范围.
分析:(1)当a=-2时,求函数f(x)=x3+3ax-1的导函数为f′(x),令f′(x)>0,求出单调增区间;令f′(x)<0求出单调减区间;
(2)若对满足-1≤a≤1的一切a的值,都有g(x)<0,变更主元,转化为关于a的一次函数,求出实数x的取值范围;
(3)依题意,x•g′(x)+lnx>0对一切x≥2恒成立,采取分离参数的方法,转化为求函数的最值问题.
解答:解:(1)当a=-2时,f′(x)=3x
2-6.令f′(x)=0得
x=±,
故当
x<-或x>
时f′(x)>0,f′(x)单调递增;
当
-<x<时f
′(x)<0,f(x)单调递减.
所以函数f′(x)的单调递增区间为(
-∞,-],[
,+∞);单调递减区间为
(-,);
(2)因f′(x)=3a
2+3a,故g(x)=3x
2-ax+3a-3.
令g(x)=h(a)=a(3-x)+3x
2-3,要使h(a)<0对满足-1≤a≤1的一切a成立,
则
| | h(-1)=3x2+x-6<0 | | h(1)=3x2-x<0 |
| |
,解得
0<x<;
0<x<.
(3)因为g(x
′)=6x-a,
所以X(6x-a)+lnx>0
即
a<6x+=h(x)对一切x≥2恒成立.
h′(x) =6+=,
令6x
2+1-lnx=φ(x),
φ′(x)=12x-.
因为x≥2,所以φ
′(x)>0,
故φ(x)在[2,+∞)单调递增,有φ(x)≥φ(2)=25-ln2>0.
因此h
′(x)>0,从而
h (x)≥h (2)=12+.
所以a
<hmin(x)=h (2)=12+.
点评:考查利用导数研究函数的单调性和最值问题,特别是恒成立问题,(2)若对满足-1≤a≤1的一切a的值,都有g(x)<0,变更主元,转化为关于a的一次函数,求出实数x的取值范围;(3)x•g′(x)+lnx>0对一切x≥2恒成立,采取分离参数的方法,转化为求函数的最值问题体现了转化的思想方法,属难题.



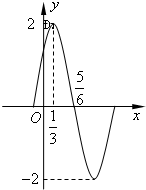 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<