
科目: 来源: 题型:
【题目】如图,四棱锥![]() 的底面是菱形,
的底面是菱形,![]() 底面
底面![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
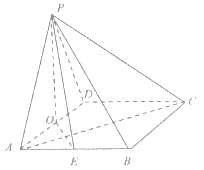
(I)证明:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在![]() 边上是否存在点
边上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,若存在,确定点
,若存在,确定点![]() 位置;若不存在,说明理由.
位置;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() 的图象上的所有的点( )
的图象上的所有的点( )
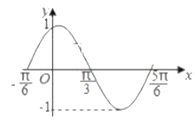
A.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目: 来源: 题型:
【题目】已知过椭圆![]() 的四个顶点与坐标轴垂直的四条直线围成的矩形
的四个顶点与坐标轴垂直的四条直线围成的矩形![]() (
(![]() 是第一象限内的点)的面积为
是第一象限内的点)的面积为![]() ,且过椭圆
,且过椭圆![]() 的右焦点
的右焦点![]() 的倾斜角为
的倾斜角为![]() 的直线过点
的直线过点![]() .
.
(1)求椭圆![]() 的标准方程
的标准方程
(2)若射线![]() 与椭圆
与椭圆![]() 的交点分别为
的交点分别为![]() .当它们的斜率之积为
.当它们的斜率之积为![]() 时,试问
时,试问![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,以
,以![]() 为切点作函数
为切点作函数![]() 图象的切线交
图象的切线交![]() 轴于点
轴于点![]() ,再过
,再过![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,
,![]() ,以此类推得点
,以此类推得点![]() ,记
,记![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)证明数列![]() 为等比数列并求出通项公式;
为等比数列并求出通项公式;
(2)设直线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,记
,记![]() (其中
(其中![]() 为坐标原点),求数列
为坐标原点),求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13,2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的60%以上,居世界第一位下表截取了2012--2016年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
高铁密度 | 9.75 | 11.49 | 17.14 | 20.66 | 22.92 |
已知高铁密度y与年份代码x之间满足关系式![]() (
(![]() 为大于0的常数)若对
为大于0的常数)若对![]() 两边取自然对数,得到
两边取自然对数,得到![]() ,可以发现
,可以发现![]() 与
与![]() 线性相关.
线性相关.
(1)根据所给数据,求y关于x的回归方程(![]() 保留到小数点后一位);
保留到小数点后一位);
(2)利用(1)的结论,预测到哪一年高铁密度会超过30千米/平方千米.
参考公式设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,
,
则回归方程![]() 的系数:
的系数: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点
是参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 取最大值时
取最大值时![]() 的值
的值
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等边三角形ABC的边长为![]() ,
,![]() 分别为
分别为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起得到四棱锥
折起得到四棱锥![]() .点P为四棱锥
.点P为四棱锥![]() 的外接球球面上任意一点,当四棱锥
的外接球球面上任意一点,当四棱锥![]() 的体积最大时,点P到平面
的体积最大时,点P到平面![]() 距离的最大值为( )
距离的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com