
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
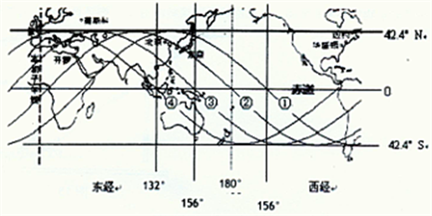
我国“神舟”六号宇宙已经发射成功,当时在飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图,如图所示,它记录了“神舟”六号飞船在地球表面垂直投影的位置变化;图中表示在一段时间内飞船绕地球圆周飞行四圈,依次飞经中国和太平洋地区的四次轨迹①、②、③、④,图中分别标出了各地点的经纬度(如:在轨迹①通过赤道时的经度为西经156°,绕行一圈后轨迹②再次经过赤道时经度为180°,……),若已知地球半径为R,地球表面处的重力加速度g,地球自转周期为24h,根据图中的信息:
(1)如果飞船运行周期用T表示,试写出飞船离地面高度的表达式。
(2)飞船运行一周,地球转过的角度是多少?
(3)求飞船运行的周期。
查看答案和解析>>
科目:高中物理 来源: 题型:
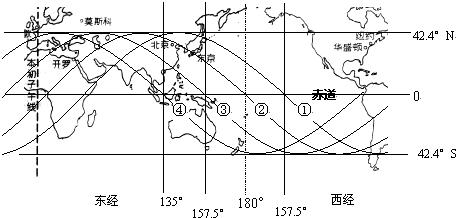
(12分)我国“神舟”六号宇宙已经发射成功,当时在飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图,如图所示,它记录了“神舟”六号飞船在地球表面垂直投影的位置变化;图中表示在一段时间内飞船绕地球圆周飞行四圈,依次飞经中国和太平洋地区的四次轨迹①、②、③、④,图中分别标出了各地点的经纬度(如:在轨迹①通过赤道时的经度为西经156°,绕行一圈后轨迹②再次经过赤道时经度为180°,……),若已知地球半径为R,地球表面处的重力加速度g,地球自转周期为24h,根据图中的信息:
(1)如果飞船运行周期用T表示,试写出飞船离地面高度的表达式。
(2)飞船运行一周,地球转过的角度是多少?
(3)求飞船运行的周期。
查看答案和解析>>
科目:高中物理 来源:2010年北京市高三上学期起点考试物理试题 题型:计算题
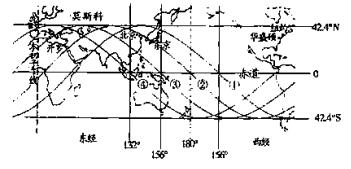
(12分)我国“神舟”六号宇宙已经发射成功,当时在飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图,如图所示,它记录了“神舟”六号飞船在地球表面垂直投影的位置变化;图中表示在一段时间内飞船绕地球圆周飞行 四圈,依次飞经中国和太平洋地区的四次轨迹①、②、③、④,图中分别标出了各地点的经纬
四圈,依次飞经中国和太平洋地区的四次轨迹①、②、③、④,图中分别标出了各地点的经纬 度(如:在轨迹①通过赤道时的经度为西经156°,绕行一圈后轨迹②再次经过赤道时经度为180°,……),若已知地球半径为R,地球表面处的重力加速度g,地球自转周期为24h,根据图中的信息:
度(如:在轨迹①通过赤道时的经度为西经156°,绕行一圈后轨迹②再次经过赤道时经度为180°,……),若已知地球半径为R,地球表面处的重力加速度g,地球自转周期为24h,根据图中的信息:
(1)如果飞船运行周期用T表 示
示 ,试写出飞船离地面高度的表达式。
,试写出飞船离地面高度的表达式。
(2)飞船运行一周,地球转过的角度是多少?
(3)求飞船运行的周期。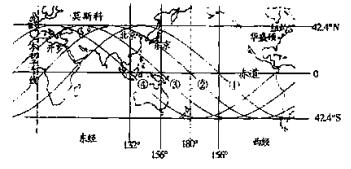
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com