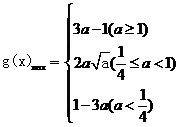浙江省杭州高中
2009届高三第六次月考
数学试题(文)
1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),本试卷满分为150分,考试时
为120分钟。
2.考试过程中不得使用计算器。
3.所有答案均做在答卷页上。
第Ⅰ卷 (选择题,共50分)
一、选择题(本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只
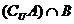 1.已知全集U={-1,0,1,2},集合A={-1,2},B={0,2},则
= ( )
1.已知全集U={-1,0,1,2},集合A={-1,2},B={0,2},则
= ( )
试题详情
A.{0} B.{2} C.{0,1,2} D.
试题详情
2.已知是实数,若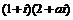 是纯虚数,则
是纯虚数,则 ( )
( )
A.-2 B.2 C.-1
D.1
试题详情
3.从3男1女4位同学中选派2位同学参加某演讲比赛,那么选派的都是男生的概率是( )
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
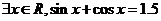 A.
B.
A.
B.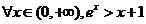
试题详情

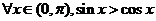 C.
D.
C.
D.
试题详情
6.函数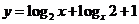 的值域是 ( )
的值域是 ( )
试题详情
试题详情
试题详情
A.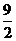 B.
B.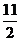 C.6
D.10
C.6
D.10
试题详情
8.若函数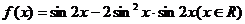 ,则
,则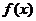 是 ( )
是 ( )
试题详情
A.最小正周期为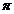 的偶函数 B.最小正周期为
的偶函数 B.最小正周期为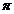 的奇函数
的奇函数
试题详情
C.最小正周期为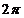 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为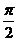 的奇函数
的奇函数
试题详情
9.利用计算器,列出自变量和函数值的对应值如下表:
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
那么方程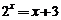 的一个根位于下列哪个区间 ( )
的一个根位于下列哪个区间 ( )
试题详情
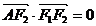 A.(0.8,1.2) B.(1.4,1.8) C.(1.8,2.2) D.(2.2,2.6)
A.(0.8,1.2) B.(1.4,1.8) C.(1.8,2.2) D.(2.2,2.6)
试题详情
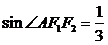 10.设F1、F2为椭圆的两个焦点,A为椭圆上的点,若已知 ,且
10.设F1、F2为椭圆的两个焦点,A为椭圆上的点,若已知 ,且
,则椭圆的离心率为
试题详情
试题详情

第Ⅱ卷 (非选择题,共100分)
试题详情
二、填空题(本大题共7小题,每小题4分,满分28分):
11.如下图,该程序运行后输出的结果为____________.
试题详情
试题详情
试题详情
试题详情
试题详情
足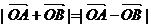 ,则实数a的值是_____________.
,则实数a的值是_____________.
试题详情
15.如下图是某几何体的三视图,其中正视图是腰长为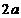 的等腰三角形俯视图是半径为
的等腰三角形俯视图是半径为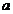 的
的
半圆,则该几何体的表面积是
.
试题详情
试题详情
16.北京2008年第29届奥运会开幕式上举行升旗仪式,
试题详情
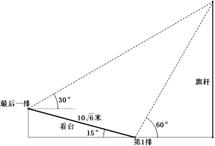 在坡度15°的看台上,同一列上的第1排和最后一排
在坡度15°的看台上,同一列上的第1排和最后一排
测得旗杆顶部的仰角分别为60°和30°,第1排和最后
试题详情
一排的距离为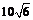 米(如图所示),旗杆底部与第1
米(如图所示),旗杆底部与第1
排在一个水平面上。若国歌长度约为50秒,升旗手
应以_______(米/秒)的速度匀速升旗.
试题详情
试题详情
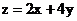 17.若x、y满足不等式组 ,且
的最小值为-6 ,则k=_______.
17.若x、y满足不等式组 ,且
的最小值为-6 ,则k=_______.
试题详情
三、解答题(本大题共5小题,满分72分,解答应写出文字说明,证明过程或演算步骤)
试题详情
已知A,B,C三点的坐标分别是A(3,0),B(0,3),C (cosθ,sinθ),其中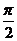 <θ<
<θ< ,
,
试题详情
且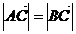 .
.
(1)求角θ的值;
试题详情
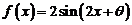 (2)当0≤x≤
(2)当0≤x≤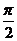 时,求函数
的最大值和最小值.
时,求函数
的最大值和最小值.
试题详情
试题详情
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
试题详情
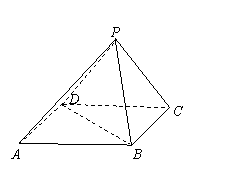 (1)求证:
(1)求证: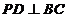 ;
;
(2)求直线BD与平面PBC所成角的正弦值.
试题详情
试题详情
已知数列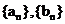 中,
中,
试题详情
(1)求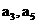 的值;
的值;
试题详情
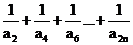 (2)求证:
(2)求证:
(3)求
的值.
试题详情
试题详情
试题详情
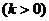 ,
,
试题详情
(1)求以O为顶点,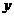 轴为对称轴,且过A,B两点的抛物线方程;
轴为对称轴,且过A,B两点的抛物线方程;
(2)设Q为抛物线准线上任意一点,过Q作抛物线的两条切线,切点分别为M,N,求
试题详情
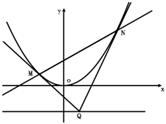 证:直线MN过一定点。
证:直线MN过一定点。
试题详情
试题详情
已知函数f(x)= 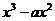 其中a为实常数.
其中a为实常数.
试题详情
(1)设当x∈(0,1)时,函数y=f(x)的图象上任一点P处的切线的斜率为k,若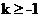 ,
,
求a的取值范围;
试题详情
(2)当x∈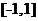 时,求函数y=f(x)
时,求函数y=f(x) 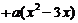 的最大值.
的最大值.
参 考 答 案
题号
1
2
3
4
5
6
7
8
9
10
选项
A
B
D
A
B
D
A
D
D
D
试题详情
二.填空题:(每题4分,共28分)
11.___45_____
12.____m>n____
13._____30_____14. ___±2______
试题详情
15._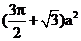 _16.___
_16.___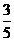 ____17. ___0______
____17. ___0______
试题详情
三、解答题:(18~20每题14分,21、22题15分,共72分)
18.解:(1)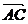 =(cosθ-3,sinθ),
=(cosθ-3,sinθ),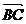 =(cosθ,sinθ-3)
2分
=(cosθ,sinθ-3)
2分
试题详情
∵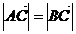 ∴
∴
化简得:sinθ=cosθ 5分
试题详情
试题详情
试题详情
试题详情
19.(Ⅰ)证明: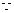 平面
平面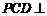 平面ABCD,
平面ABCD,
试题详情
又平面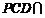 平面ABCD=CD,
平面ABCD=CD,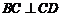 ,
,
试题详情
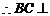 平面PCD,
--------------------------4分
平面PCD,
--------------------------4分
试题详情
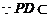 平面PCD,
平面PCD,
试题详情
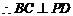 ;
--------------------------6分
;
--------------------------6分
(2)取PC中点F,连接DF、BF,
试题详情
由(1)知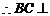 平面PCD, 又因为
平面PCD, 又因为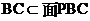 ,
,
试题详情
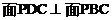 所以
------------------------8分
所以
------------------------8分
试题详情
因为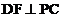 所以
所以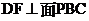 所以BF为BD在面PBC内的射影
所以BF为BD在面PBC内的射影
试题详情
所以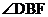 为BD与平面PBC所成角------------------------12分
为BD与平面PBC所成角------------------------12分
试题详情
试题详情
20.(1) 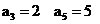 ------------------------4分
------------------------4分
试题详情
(2)由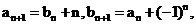 可得
可得
试题详情
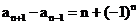 ------------------------6分
------------------------6分
试题详情
所以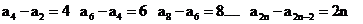 ------------------------8分
------------------------8分
试题详情
将上述式子相加得 
试题详情
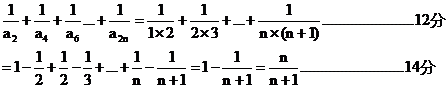
 (或者用数学归纳法证明)------------------------10分
(或者用数学归纳法证明)------------------------10分
(3)
试题详情
21.解:(1)设抛物线方程为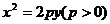 ,AB的方程为
,AB的方程为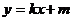 ,
,
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
22.解:(1) ∵k=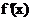 =3
=3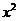 -2ax,x∈(0,1) -------------1分
-2ax,x∈(0,1) -------------1分
试题详情
k≥1,得3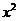 -2ax+1≥0,即a≤
-2ax+1≥0,即a≤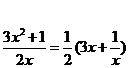 恒成立.-------------3分
恒成立.-------------3分
试题详情
∴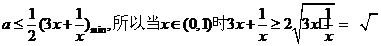
试题详情
试题详情
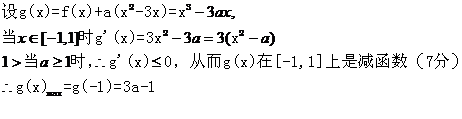 (2)
(2)
试题详情
试题详情
得
试题详情
试题详情
∴g(x)的极大值为g(-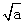 )=2
)=2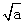 ,
,
试题详情

3>当a≤0时,g’(x)≥0,从而g(x)在[-1,1]上是增函数,
试题详情
∴
试题详情
试题详情