
芜湖市2009届高中毕业班模拟考试
数学试卷(理科)
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
注意事项:
1.答卷前,考生务必用2B铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试题卷上。
3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
4.参考公式:
第I卷(选择题)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.集合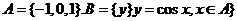 ,则
,则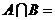
A.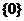 B.
B.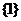 C.
C.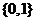 D.
D.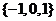
2.复数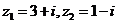 ,则复数
,则复数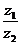 在复平面内对应的点位于
在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.命题“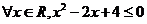 ”的否定为
”的否定为
A.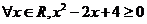 B.
B.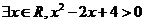
C.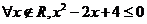 D.
D.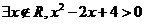
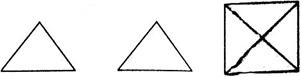 4.如图所示是一个简单几何体的三视图,其正视图与侧视图是边长为2的正三角形,俯视
4.如图所示是一个简单几何体的三视图,其正视图与侧视图是边长为2的正三角形,俯视
图为正方形,则其体积是
A.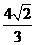 B.
B.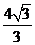
C.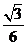 D.
D.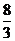 正视图
侧视图
俯视图
正视图
侧视图
俯视图
5.将直线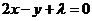 沿
沿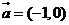 平移后,所得直线与圆
平移后,所得直线与圆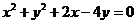 相切实数
相切实数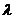 的值为
的值为
A.-3
B.
6.下列四个命题正确的是
①线性相关系数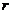 越大,两个变量的线性相关性越强;反之,线性相关性越小;
越大,两个变量的线性相关性越强;反之,线性相关性越小;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数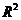 来刻画回归效果,
来刻画回归效果,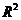 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
④随机误差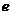 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足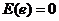
A.①③ B.②④ C.①④ D.②③
7.已知两个不同的平面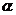 、
、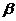 和两条不重合的直线
和两条不重合的直线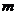 、
、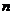 则下列四个命题不正确的是
则下列四个命题不正确的是
A.若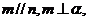 则
则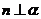
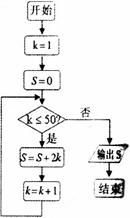 B.若
B.若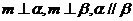
C.若 则
则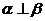
D.若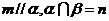 ,则
,则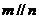
8.如果执行右图的程序框图,那么输出的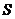 =
=
A.2450 B.2500
C.2550 D.2652
9.在周长为16的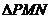 中,
中, ,则
,则 的取值
的取值
范围是
A.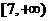 B.(0,16)
B.(0,16)
B.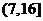 D.
D.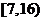
10.以下四个命题中,正确的个数是
①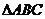 中,
中,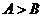 的充要条件是
的充要条件是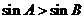 ;
;
②函数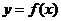 在区间(1,2)上存在零点的充要条件是
在区间(1,2)上存在零点的充要条件是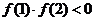 ;
;
③等比数列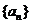 中,
中,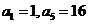 ,则
,则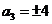 ;
;
④把函数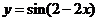 的图象向右平移2个单位后,得到的图象对应的解析式为
的图象向右平移2个单位后,得到的图象对应的解析式为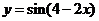
A.1
B.
11.设实数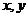 满足
满足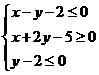 ,则
,则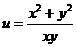 的取值范围是
的取值范围是
A.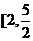 ] B.
] B.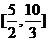 C.
C.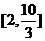 D.
D.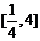
12.幂指函数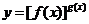 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得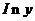
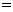
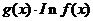 ,两边同时求导得
,两边同时求导得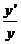 =
= ,于是
,于是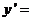
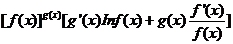 ,运用此方法可以探求得知
,运用此方法可以探求得知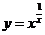 的一个单调递增区间为
的一个单调递增区间为
A.(0,2) B.(2,3) C.(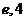 ) D.(3,8)
) D.(3,8)
第Ⅱ卷(非选择题)
二、填空题(本大题共4小题,每小题4分,共16分)
13. 的展开式中
的展开式中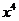 项的系数为210,则实数
项的系数为210,则实数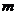 的值为______________
的值为______________
14.已知极坐标系的极点在直角坐标系的原点,极轴与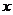 正半轴重合,则由曲线
正半轴重合,则由曲线
 和
和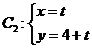 (
(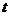 为参数)围成的平面图形的面积是________
为参数)围成的平面图形的面积是________
15.在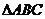 中,
中,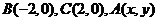 ,给出
,给出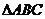 满足的条件,就能得到动点
满足的条件,就能得到动点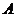 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
条件
方程
①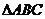 周长为10
周长为10
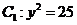
②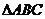 面积为10
面积为10
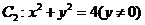
③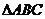 中,
中,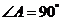
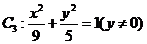
则满足条件①、②、③的轨迹方程分别为________(用代号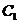 、
、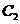 、
、 填入)
填入)
16.设数列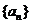 的前
的前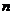 项和为
项和为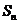 ,且
,且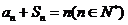 ,则数列
,则数列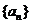 的通项公式是_______________。
的通项公式是_______________。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)
已知函数 其中
其中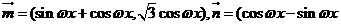
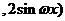 其中
其中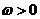 ,若
,若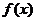 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于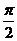 。
。
(I)求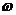 的取值范围;
的取值范围;
(Ⅱ)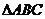 中,
中,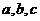 分别是角
分别是角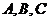 的对边,
的对边, 当
当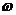 最大时,
最大时,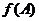 =1,求
=1,求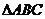 的面积。
的面积。
18.(本题满分12分)
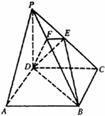
如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱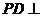 底面
底面
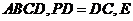 是
是 的中点,作
的中点,作 交
交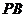 于点
于点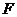 。
。
 (I)证明:
(I)证明: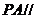 平面
平面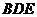 ;
;
(Ⅱ)证明: 平面
平面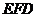 ;
;
(Ⅲ)求二面角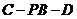 的大小。
的大小。
19.(本题满分12分)
(I)求选出的4人均为选《极坐标系与参数方程》的概率;
在“自选专题”考试中,某考场的每位同学都从《不等式选讲》和《极坐标系与参数方程》两专题中只选了一道数学题,第一小组选《不等式选讲》的有1人,选《极坐标系与参数方程》的有5人,第二小组选《不等式选讲》的有2人,选《极坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况。
(Ⅱ)设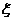 为选出的4个人中选《不等式选讲》的人数,求
为选出的4个人中选《不等式选讲》的人数,求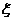 的分布列和数学期望。
的分布列和数学期望。
20.(本题满分12分)
已知函数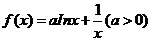
(I)求函数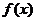 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若对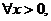 均有
均有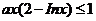 成立,求实数
成立,求实数 的取值范围。
的取值范围。
21.(本题满分12分)
已知二次函数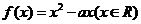 同时满足:①方程
同时满足:①方程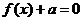 有且只有一个根;②在定义域内在
有且只有一个根;②在定义域内在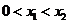 ,使得不等式
,使得不等式 成立;设数列
成立;设数列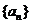 的前
的前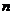 项和
项和 。
。
(I)求数列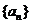 的通项公式;
的通项公式;
(Ⅱ)设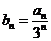 ,求数列
,求数列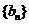 的前
的前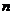 项和
项和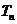 ;
;
(Ⅲ)证明:当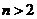 时,
时,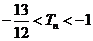 。
。
22.(本题满分14分)
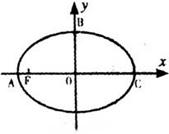
已知椭圆 的左焦点为
的左焦点为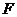 ,左右顶点分别为
,左右顶点分别为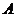 ,
,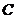 ,上顶点为
,上顶点为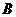 ,过
,过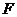 ,
,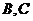 三点作⊙M,其中圆心
三点作⊙M,其中圆心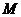 的坐标为(
的坐标为(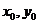 )。
)。
(I)若⊙M的圆心在直线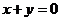 上,求椭圆
上,求椭圆 的方程。
的方程。
(Ⅱ)若 、
、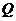 是椭圆
是椭圆 上满足
上满足 的两点,求证:
的两点,求证: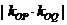 是定值。
是定值。
芜湖市2009届高中毕业班模拟考试
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.B 2.A 3.B 4.B 5.C 6.B 7.D 8.C 9.D 10.A 11.C 12.A
二、填空题(本大题共4小题,每小题4分,共16分)
13. 14.18
15.
14.18
15. 、
、 、
、 16.
16.
三、解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。)
17.解:(Ⅰ)
=
 函数
函数 的周期
的周期 ,
,
由题意可知 即
即 ,
,
解得 ,即
,即 的取值范围是
的取值范围是
(Ⅱ)由(Ⅰ)可知
而
由余弦定理知
 又
又 ,
,


18.(I)证明:连结 交
交 于
于 ,连结
,连结
 底面
底面 是正方形,
是正方形, 点
点 是
是 的中点,
的中点,
在 中,
中, 是中位线,
是中位线, ,
,
而 平面
平面 且
且 平面
平面 ,所以,
,所以, 平面
平面
(Ⅱ)证明: 底面
底面 且
且 底面
底面 ,
,
 ,可知
,可知 是等腰直角三角形,而
是等腰直角三角形,而 是斜边
是斜边 的中线。
的中线。
 ①
①
同样由 底面
底面 得
得
 底面
底面 是正方形,有
是正方形,有 平面
平面 。
。
而 平面
平面 ②
②
由①和②推得 平面
平面
而 平面
平面
又 且
且 ,所以
,所以 平面
平面
(Ⅲ)解:由(Ⅱ)知, ,故
,故 是二面角
是二面角 的平面角
的平面角
由(2)知,
设正方形 的边长为
的边长为 ,则
,则



在 中,
中,
在 中,
中,

所以,二面角 的大小为
的大小为
方法二;如图所示建立空间直角坐标系,D为坐标原点,设
(I)证明:连结AC,AC交BD于G,连结EG。
依题意得A( ,0,0),P(0,0,
,0,0),P(0,0,  ),
),
 底面
底面 是正方形,
是正方形, 是此正方形的中心,故点
是此正方形的中心,故点 的坐标为
的坐标为 )
)
且 ,这表明
,这表明
而 平面
平面 且
且 平面
平面 平面
平面
(Ⅱ)证明:依题意得 ,
,
又 ,故
,故
由已知 ,且
,且 ,所以
,所以 平面
平面
(Ⅲ)解:设点 的坐标为
的坐标为 ,则
,则
 则
则

从而 所以
所以

由条件 知,
知, ,即
,即
 ,解得
,解得
 点
点 的坐标为
的坐标为 ,且
,且

即 ,故
,故 二面角
二面角 的平面角。
的平面角。
 ,且
,且


所以,二面角 的大小为
的大小为 (或用法向量求)
(或用法向量求)
19.解:(I)设“从第一小组选出的2人均考《极坐标系与参数方程》”为事件A,“从第二小组选出的2人均考《极坐标系与参数方程》”为事件B,由于事件A、B相互独立,
且
所以选出的4人均考《极坐标系与参数方程》的概率为

(Ⅱ)设 可能的取值为0,1,2,3,得
可能的取值为0,1,2,3,得


 的分布列为
的分布列为

0
1
2
3





 的数学期望
的数学期望
20.解:由题意
(I)当 时。
时。
由 得
得 ,解得
,解得 ,函数
,函数 的单调增区间是
的单调增区间是 ;
;
由 得
得 ,解得
,解得 ,函数
,函数 的单调减区间是
的单调减区间是
 当
当 时,函数
时,函数 有极小值为
有极小值为
(2) 当 时,由于
时,由于 ,均有
,均有 ,
,
即 恒成立,
恒成立,
 ,
,
由(I)知函数 极小值即为最小值,
极小值即为最小值,
 ,解得
,解得
21.解(I) 方程
方程 有且只有一个根,
有且只有一个根, 或
或
又由题意知 舍去
舍去
当 时,
时,
当 时,
时, 也适合此等式
也适合此等式

(Ⅱ)
 ①
①
 ②
②
由①-②得


(Ⅲ)法一:当 2时,
2时,
 时,数列
时,数列 单调递增,
单调递增,
又由(II)知

法二:当 时,
时,



22.(I)⊙M过点 三点,
三点, 圆心
圆心 既在
既在 的垂直平分线上,也在
的垂直平分线上,也在 的垂直平分线上,
的垂直平分线上, 的垂直平分线方程为
的垂直平分线方程为
 的中点为
的中点为
 的垂直平分线方程为
的垂直平分线方程为
由④⑤得 即
即
 在直线
在直线 上。
上。
 由
由 得
得
 椭圆的方程为
椭圆的方程为
(Ⅱ)设 则
则

 是定值;
是定值;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com