山东省枣庄市
2009届高三年级调研考试
数学试题(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目、试类类型用2B铅笔涂写在答题卡上。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用像皮擦干净后,再选涂其他答案,不能答在试题卷上。
3.考试结束后,监考人员将第II卷和答题卡一并收回。
参考公式:
锥体体积公式 其中S为底面面积、h为高
其中S为底面面积、h为高
球的表面积公式 其中R表示球的半径
其中R表示球的半径
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
一、选择题:本大题共12小题,每小 题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知 则 ( )
则 ( )
试题详情
A. B.
B.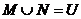
试题详情
C. D.
D.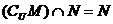
试题详情
2.设复数 是实数,则实数
是实数,则实数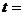
( )
试题详情
试题详情
|
试题详情
A.是 的图象 的图象 试题详情
B.是 的图象 的图象 试题详情
C.是 的图象 的图象 D.以上说法都不对 试题详情
4.已知 的 ( ) 的 ( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 试题详情
5.设函数 ( ) ( ) A.3 B.4 C.7 D.9 试题详情
6.一个几何体的三视图如右图所示,则该几何体外接球的表面积为 ( ) 试题详情
|
试题详情
C. D.以上都不对 D.以上都不对 试题详情
7.不等式 的解集是 ( ) 的解集是 ( ) 试题详情
A. 试题详情
B.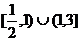 试题详情
C. 试题详情
D.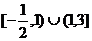 试题详情
8.已知 的三个内角A,B,C的对边,向量 的三个内角A,B,C的对边,向量 周长的最小值为 ( ) 周长的最小值为 ( ) 试题详情
试题详情
9.现有10个数,其平均数是3,且这10个数的平方和是100,那么这个数组的标准差是( ) A.1 B.2 C.3 D.4 试题详情
10.已知 的值是 ( ) 的值是 ( ) 试题详情
试题详情
试题详情
试题详情
|
试题详情
A. B. B.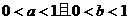 试题详情
C. D. D.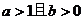 第Ⅱ卷(非选择题 共90分) 注意事项: 试题详情
试题详情
2.答卷前请将密封线内的项目填写清楚。 把答案写在题中的横线上。 试题详情
二、填空题:本大题共4小题,每小题4分,共16分。 13.设椭圆 的右焦点与抛物线 的右焦点与抛物线 的 的 试题详情
焦点相同,离心率为 ,则此椭圆的标准方程为
。 ,则此椭圆的标准方程为
。 试题详情
试题详情
15.已知 。
。 试题详情
16.设 的最大值为 。 的最大值为 。 说明、证明过程或演算步骤。 试题详情
三、解答题:本大题共6小题,共74分,解答应写出文字
试题详情
已知函数 试题详情
试题详情
(1)求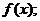 试题详情
(2)当 的值域。 的值域。 试题详情
18.(本小题满分12分) 先后抛掷两枚骰子,每次各1枚,求下列事件发生的概率: (1)事件A:“出现的点数之和大于3”; (2)事件B:“出现的点数之积是3的倍数”。 试题详情
试题详情
|
试题详情
(1)证明:平面 平面PAB; 平面PAB; (2)求二面角A―BE―P的大小。 试题详情
试题详情
设数列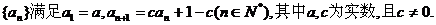 试题详情
(1)求数列 的通项公式; 的通项公式; 试题详情
(2)设 ,求数列 ,求数列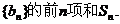 试题详情
试题详情
已知 的顶点A、B在椭圆 的顶点A、B在椭圆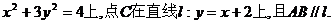 试题详情
(1)当AB边通过坐标原点O时,求AB的长及 的面积; 的面积; 试题详情
(2)当 ,且斜边AC的长最大时,求AB所在直线的方程。 ,且斜边AC的长最大时,求AB所在直线的方程。 试题详情
|
试题详情
试题详情
设函数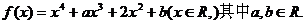 试题详情
(1)当 的单调性; 的单调性; 试题详情
(2)若函数 的取值范围; 的取值范围; 试题详情
(3)若对于任意的 上恒成立,求 上恒成立,求 的取值范围。 的取值范围。 试题详情
一、选择题:本大题共12小题,每小题5分,共60分。 BADD CCCB AADB 二、填空题:本大题共4小 题,每小题4分,共16分。 13. 14. 15.-2 16.73
20090406 17.解:(1) 2分 2分  4分 4分    6分 6分 (2) 根据正弦函数的图象可得: 当 时, 时,  取最大值1 8分 取最大值1 8分 当 时 时  10分 10分  即 12分 12分 18.解:先后抛掷两枚骰子可能出现的情况:(1,1),(1,2),(1,3),…,(1,6);(2,1)(2,2),(2,3),…,(2,6);…;(6,1),(6,2),(6,3),…,(6,6),基本事件总数为36。 2分 (1)在上述基本事件中,“点数之和等于3”的事件只有(1,2),(2,1)两个可能,点数之和等于2的只有(1,1)一个可能的结果,记点数之和不大于3为事件A1,则事件A1发生的概率为: 4分 4分  事件“出现的点数之和大于3”发生的概率为 事件“出现的点数之和大于3”发生的概率为  7分 7分 (2)与(1)类似,在上述基本事件中,“点数之积是3的倍数”的事件有20个可能的结果。 所以事件“出现的点数之积是3的倍数”发生的概率为  12分 12分

 BCD是等边三角形, BCD是等边三角形,  E是CD的中点, E是CD的中点, 而AB//CD, 2分 2分 又 平面ABCD, 平面ABCD,  而呵呵平面PAB。 4分 又 平面PAB。 6分 平面PAB。 6分 (2)由(1)知, 平面PAB,所以 平面PAB,所以 又 是二面角A―BE―P的平面角 9分 是二面角A―BE―P的平面角 9分  平面ABCD, 平面ABCD,  在  故二面角A―BE―P的大小是 12分 12分 20.解:(1)  是首项为 是首项为 的等比数列 2分 的等比数列 2分  4分 4分 当 仍满足上式。 仍满足上式。  注:未考虑 的情况,扣1分。 的情况,扣1分。 (2)由(1)得,当 时, 时,  8分 8分   两式作差得    12分 12分 21.解:(1)因为 且AB通过原点(0,0),所以AB所在直线的方程为 且AB通过原点(0,0),所以AB所在直线的方程为 由 得A、B两点坐标分别是A(1,1),B(-1,-1)。 得A、B两点坐标分别是A(1,1),B(-1,-1)。

又 的距离。 的距离。  4分 4分 (2)设AB所在直线的方程为 由 因为A,B两点在椭圆上,所以  即 5分 5分 设A,B两点坐标分别为 ,则 ,则  且 6分 6分   8分 8分 又 的距离, 的距离, 即 10分 10分   边最长。(显然 边最长。(显然 ) ) 所以AB所在直线的方程为 12分 12分 22.解:(1) 当 令 3分 3分 当 的变化情况如下表: 的变化情况如下表:  
0 


2 

- 0 + 0 - 0 + 
单调递减 极小值 单调递增 极大值 单调递减 极小值 单调递增 所以 上是增函数, 上是增函数, 在区间 上是减函数 6分 上是减函数 6分 (2) 的根。 的根。  处有极值。 处有极值。 则方程 有两个相等的实根或无实根, 有两个相等的实根或无实根,  8分 8分 解此不等式,得 这时, 是唯一极值。 是唯一极值。 因此满足条件的 10分 10分 注:若未考虑 进而得到 进而得到 ,扣2分。 ,扣2分。 (3)由(2)知,当 恒成立。 恒成立。 当 上是减函数, 上是减函数, 因此函数 12分 12分 又 上恒成立。 上恒成立。  于是 上恒成立。 上恒成立。  因此满足条件的 14分 14分
| | | | | | | | | | | | | | | |

 其中S为底面面积、h为高
其中S为底面面积、h为高 其中R表示球的半径
其中R表示球的半径 则 ( )
则 ( ) B.
B.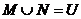
 D.
D.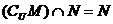
 是实数,则实数
是实数,则实数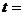
 B.
B. C.
C. D.
D.