|

试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情

的数表,若表中每行的7个数自左至右依次都成等差 数列,每列的7个数自上而下依次也都成等差数列, 试题详情
且正中间的数a =1,则表中所有数的和为_____. =1,则表中所有数的和为_____. 试题详情
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤 16、(本小题满分12分)如图所示,以向量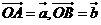 为边 为边 试题详情
试题详情
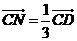 . .
试题详情
(1)用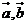 表示 表示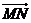 ; ; 试题详情
(2)若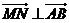 ,求 ,求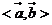 的最大值. 的最大值. 试题详情
17、(本小题满分12分)已知袋中有编号为1~9的小球各一个,它们的大小相同,从中任取三个小球.求: (Ⅰ)恰好有一球编号是3的倍数的概率; (Ⅱ)至少有一球编号是3的倍数的概率; (Ⅲ)三个小球编号之和是3的倍数的概率. 试题详情
18、(本小题满分14分)已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4. (Ⅰ)求椭圆的方程; 试题详情
(Ⅱ)直线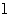 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程. 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程. 试题详情
19、(本小题满分14分)(Ⅰ)试讨论方程(1-k)x2+(3-k2)y2=4(k∈R)所表示的曲线; 试题详情
(Ⅱ)设双曲线的中心在原点,准线平行于x轴,离心率为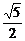 ,且点P(0,5)到此双曲线上的点的最近距离为2,求双曲线的方程. ,且点P(0,5)到此双曲线上的点的最近距离为2,求双曲线的方程. 试题详情
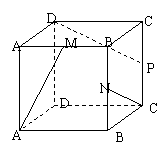 20、(本小题满分14分)已知在棱长为1的正方体 20、(本小题满分14分)已知在棱长为1的正方体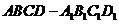 中, 中,
试题详情
M,N,P分别为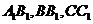 的中点。求异面直线 的中点。求异面直线 所成的角。 试题详情
21、(本小题满分14分)对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点 已知函数f(x)=ax2+(b+1)x+(b?1)(a≠0) 已知函数f(x)=ax2+(b+1)x+(b?1)(a≠0) (1)若a=1,b=?2时,求f(x)的不动点; (2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围; 试题详情
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B关于直线y=kx+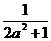 对称,求b的最小值 对称,求b的最小值 湖南省衡阳市祁东县育贤中学高三文科数学试题(2007年1月) 试题详情
一、
选择题: 1、答案:D 解:②表示垂直于同一平面的两条直线互相平行; ③表示垂直于同一直线的两个平面互相平行; 2、答案:D ; 解: ,非P真;又 ,非P真;又 真,所以选D; 真,所以选D; 3、答案:B ; 解: 本题考查了正方体堆垒问题及数列通项公式的求解.列出该数列的前几项,通过相邻项间的关系可得出该数列的规律而得出一等差数列. 本题考查了正方体堆垒问题及数列通项公式的求解.列出该数列的前几项,通过相邻项间的关系可得出该数列的规律而得出一等差数列. 由图示可得,该正方体的个数所组成的数列1,3,6,…,
其后一项减前一项得一数列2,3,4,…为一个等差数列.由此可得第6层的正方体的个数为1,3,6,10,15,21,… , 故应选B. 4、答案:D ; 解: 的图象向右平移 的图象向右平移 单位后得到: 单位后得到: ,故选D; ,故选D; 5、答案:B ; 解:据题意可知集合A表示函数 的定义域, 的定义域, ,易化简得 ,易化简得 ,由于B ,由于B A,故当 A,故当 时,即 时,即 时易知符合题意;当 时易知符合题意;当 时, 时, ,要使B ,要使B A,结合数轴知需 A,结合数轴知需 或 或 (经验证符合题意)或 (经验证符合题意)或 (经验证不合题意舍去),解得 (经验证不合题意舍去),解得 ,故综上所述可知满足条件的 ,故综上所述可知满足条件的 的取值范围是 的取值范围是 ,故答案为B; ,故答案为B; 6、答案:D ; 解:由图象变换可以得到两个图象间的关系,函数 是由函数 是由函数 的图象向右平移一个单位得到,而 的图象向右平移一个单位得到,而 是由函数 是由函数 的图象关于y轴对称得到 的图象关于y轴对称得到 再向右平移一个单位得到,故两函数的图象关于直线 再向右平移一个单位得到,故两函数的图象关于直线 对称。故选D 对称。故选D 7、答案:B ; 解:两直线平行,则其斜率相等,利用两点间直线的斜率公式可以得两字母 间的关系,于是可得两点间的距离. 间的关系,于是可得两点间的距离. 由题意得 所以 故应选B. 故应选B. 8、答案:B ; 解:由于 ,故函数的定义域为 ,故函数的定义域为 ,根据已知0<a<b<c,则易将函数解析式化简为 ,根据已知0<a<b<c,则易将函数解析式化简为 = =  ,故 ,故 且其定义域关于原点对称,即函数为偶函数,其图象关于y轴对称。故应选B. 且其定义域关于原点对称,即函数为偶函数,其图象关于y轴对称。故应选B. 9、答案:C ; 解:本题考查直线的斜率,由垂直关系得两直线的斜率之积为 ,再由均值不等式转化转化得出不等关系式,分类讨论得出 ,再由均值不等式转化转化得出不等关系式,分类讨论得出 的最小值.由题意 的最小值.由题意 , , ∵两直线互相垂直, ∴ ,即 ,即 , , ∴ ,则 ,则 . . 当 时, 时, ;当 ;当 时, 时, . . 综合得 的最小值为 的最小值为 . 故应选C. . 故应选C. 10、答案:C ; 解:由题意可知,存在 ,使 ,使 ,即 ,即 ,从函数定义出发,画出映射帮助思考,从A到B再到C是由题意可得,如果继续对C集合中的 ,从函数定义出发,画出映射帮助思考,从A到B再到C是由题意可得,如果继续对C集合中的 ,应用法则 ,应用法则 ,则会得到 ,则会得到 ,从B到C再到D的映射为 ,从B到C再到D的映射为 ,即存在 ,即存在 ,使 ,使 ,即函数 ,即函数 过点 过点 ,即方程 ,即方程 有解,易知 有解,易知 在实数集R上无解故选D。 在实数集R上无解故选D。 二、
填空题: 11、答案:1 ; 解:根据集合中元素的确定性,我们不难得到两集合的元素是相同的,这样需要列方程组分类讨论,显然复杂又烦琐.这时若能发现0这个特殊元素,和 中的a不为0的隐含信息,就能得到如下解法.由已知得 中的a不为0的隐含信息,就能得到如下解法.由已知得 =0,及a≠0,所以b=0,于是a2=1,即a=1或a=-1,又根据集合中元素的互异性a=1应舍去,因而a=-1,故a2008+b2008=(-1) 2008=1. =0,及a≠0,所以b=0,于是a2=1,即a=1或a=-1,又根据集合中元素的互异性a=1应舍去,因而a=-1,故a2008+b2008=(-1) 2008=1. 12、答案:120度; 解:依题意可知: A、O、B、C构成平形四边形, A、O、B、C构成平形四边形, ,故 ,故 的内角C为120度; 的内角C为120度; 13、答案: ; ; 解:    . .
14、答案: ; ; 解: ,设 ,设 ,依题意可知: ,依题意可知: ,又P在曲线上,故 ,又P在曲线上,故 ,故点P的坐标为 ,故点P的坐标为 ; ; 15、答案:49 ; 解:本题考查用取特殊值法进行验证.由题意分析, 不妨设各个格中的数都为1,
则符合题意要求,所以表中所有数字之和为49. 三、
解答题: 16、 解:(1)因为
 , ,
所以 . .
(2)由 即 即 , , 亦即 . . 故 , , 当且仅当 时取得等号. 时取得等号. 又 . . 故当 时有 时有 有最大值 有最大值 . . 17、 解:(Ⅰ)从九个小球中任取三个共有 种取法,它们是等可能的.设恰好有一球编号是3的倍数的事件为A, 种取法,它们是等可能的.设恰好有一球编号是3的倍数的事件为A, 则 . . (Ⅱ)设至少有一球编号是3的倍数的事件为B, 则 . . (Ⅲ)设三个小球编号之和是3的倍数的事件为C,设集合 , ,  ,则取出三个小球编号之和为3的倍数的取法共有 ,则取出三个小球编号之和为3的倍数的取法共有 种,则 种,则 . . 18、解:设椭圆方程为 (Ⅰ)易得所求椭圆方程为 . . (Ⅱ)解法一:由题意知直线 的斜率存在,设直线 的斜率存在,设直线 的方程为 的方程为 由 ,消去y得关于x的方程: ,消去y得关于x的方程: 由直线 与椭圆相交于A、B两点, 与椭圆相交于A、B两点, 解得 解得 又由韦达定理得   原点 原点 到直线 到直线 的距离 的距离  . . 对 两边平方整理得: 两边平方整理得: (*)∵ (*)∵ , ,  整理得: 整理得: 又 又 , , 从而 从而 的最大值为 的最大值为 ,此时代入方程(*)得 ,此时代入方程(*)得  
所以,所求直线方程为: . . 19、(Ⅰ)解:(1)3-k2>1-k>0 k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; (2) 1-k>3-k2>0 k∈(- k∈(- ,-1),方程所表示的曲线是焦点在y轴上的椭圆; ,-1),方程所表示的曲线是焦点在y轴上的椭圆; (3)1-k=3-k2>0 k=-1,表示的是一个圆; k=-1,表示的是一个圆; (4)(1-k)(3-k2)<0 k∈(-∞,- k∈(-∞,- )∪(1, )∪(1, ),表示的是双曲线; ),表示的是双曲线; (5)k=1,k=- ,表示的是两条平行直线;k= ,表示的是两条平行直线;k= ,表示的图形不存在. ,表示的图形不存在. (Ⅱ)解:依题意,设双曲线的方程为 - - =1(a>0,b>0).∵e= =1(a>0,b>0).∵e= = = ,c2=a2+b2,∴a2=4b2. ,c2=a2+b2,∴a2=4b2. 设M(x,y)为双曲线上任一点,则|PM|2=x2+(y-5)2=b2( -1)+(y-5)2= -1)+(y-5)2= (y-4)2+5-b2(|y|≥2b). (y-4)2+5-b2(|y|≥2b). ①若4≥2b,则当y=4时,|PM|min2=5-b2=4,得b2=1,a2=4.从而所求双曲线方程为 -x2=1. -x2=1. ②若4<2b,则当y=2b时,|PM|min2=4b2-20b+25=4,得b= (舍去b= (舍去b= ),b2= ),b2= ,a2=49. ,a2=49. 从而所求双曲线方程为 - - =1. =1. 20、解:如图,连结 ,由 ,由 为 为 中点,则 中点,则 从而 从而 .故AM和 .故AM和 所成的角为 所成的角为 所成的角,易证 所成的角,易证 ≌ ≌ 。所以 。所以 ,故 ,故 所成的角为 所成的角为 。又设AB的中点为Q,则 。又设AB的中点为Q,则 又 又 从而CN与AM所成的角就是 从而CN与AM所成的角就是 (或其补角)。易求得 (或其补角)。易求得 在 在 中,由余弦定理得 中,由余弦定理得 ,故 ,故 所成的角为 所成的角为 。 。 21、解 (1)当a=1,b=?2时,f(x)=x2?x?3, (1)当a=1,b=?2时,f(x)=x2?x?3, 由题意可知x=x2?x?3,得x1=?1,x2=3 故当a=1,b=?2时,f(x)的两个不动点为?1,3 (2)∵f(x)=ax2+(b+1)x+(b?1)(a≠0)恒有两个不动点, ∴x=ax2+(b+1)x+(b?1), 即ax2+bx+(b?1)=0恒有两相异实根 ∴Δ=b2?4ab+4a>0(b∈R)恒成立 于是Δ′=(4a)2?16a<0解得0<a<1 故当b∈R,f(x)恒有两个相异的不动点时,0<a<1 (3)由题意A、B两点应在直线y=x上,设A(x1,x1),B(x2,x2) 又∵A、B关于y=kx+ 对称 对称 ∴k=?1 设AB的中点为M(x′,y′) 设AB的中点为M(x′,y′) ∵x1,x2是方程ax2+bx+(b?1)=0的两个根 ∴x′=y′= , , 又点M在直线 上有 上有 , , 即 ∵a>0,∴2a+ ≥2 ≥2 当且仅当2a= 当且仅当2a= 即a= 即a= ∈(0,1)时取等号, ∈(0,1)时取等号, 故b≥? ,得b的最小值? ,得b的最小值?  作者: 湖南省衡阳市祁东县育贤中学 高明生 彭铁军 PC: 421600 TEL: 0734---6184532 Cellphone: 13187168216 E―mail: hunanqidonggms@163.com QQ: 296315069
| 
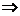 x//y”为真命题的是( ) ①x,y,z均为直线; ②x,y是直线,z是平面
x//y”为真命题的是( ) ①x,y,z均为直线; ②x,y是直线,z是平面 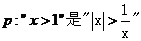 的充要条件;命题
的充要条件;命题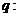 若
若 的解集为
的解集为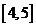 ,
,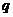 ”为假 B、“P且
”为假 B、“P且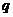 ”为真 C、“P且?
”为真 C、“P且?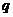 ”为真 D、“?P且
”为真 D、“?P且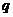 ”为真
”为真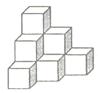
 则下列结论中正确的是( )
则下列结论中正确的是( )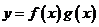 的周期为
的周期为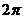 ;
;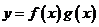 的最大值为1;
的最大值为1;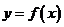 的图象向左平移
的图象向左平移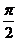 单位后得
单位后得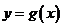 的图象;
的图象;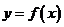 的图象向右平移
的图象向右平移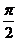 单位后得
单位后得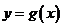 的图象;
的图象;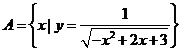 ,
,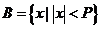 ,若B
,若B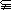 A,则实数
A,则实数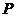 的取值范围是( )
的取值范围是( )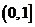 B、
B、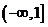 C、
C、 D、
D、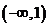
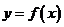 定义在实数集上,则函数
定义在实数集上,则函数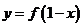 与
与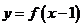 的图象关于( )
的图象关于( )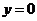 对称 B、直线
对称 B、直线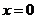 对称 C、直线
对称 C、直线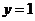 对称 D、直线
对称 D、直线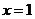 对称
对称 C.2 D.不能确定
C.2 D.不能确定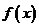 =
=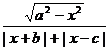 (0<a<b<c)的图象关于( )对称
(0<a<b<c)的图象关于( )对称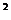 y+1=0与直线(a
y+1=0与直线(a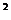 +1)x-by+3=0互相垂直,a,b∈R,则|ab|的最小值是( )
+1)x-by+3=0互相垂直,a,b∈R,则|ab|的最小值是( )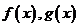 都是定义在实数集R上的函数,且方程
都是定义在实数集R上的函数,且方程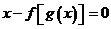 有实数解,则
有实数解,则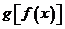 不可能是( )
不可能是( )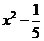 B、
B、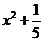 C、
C、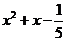 D、
D、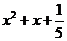
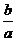 ,1},也可表示为{a2,a+b,0},则a2008+b2008=
.
,1},也可表示为{a2,a+b,0},则a2008+b2008=
.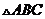 的外心,且
的外心,且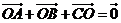 ,则
,则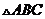 的内角C为
度;
的内角C为
度;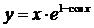 的导数为
。
的导数为
。 在点P处的切线平行于直线
在点P处的切线平行于直线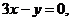 则点P的坐标为
;
则点P的坐标为
;