S=0 i=1 WHILE i<=3 S=S+2*i i=i+1 WEND PRINT S
13.正方体AC1中,AC1与A1D所成角等于____________。
试题详情
二、填空题(每题4分,共16分)
14.向量 =(-2,3), =(-2,3), =(1,m),若 =(1,m),若 、 、 夹角为钝角,则实数 夹角为钝角,则实数 m的范围是_________。
15.右边程序运行结果输出S的值是_________。
16.已知实数x,y满足x2+y2≤1,x+y≤0,则z=x+2y的最大值是___________。
17.(本小题满分12分) 试题详情
三、解答题(共5个小题,满分64分,写出必要的过程及文字说明)
试题详情
试题详情
18.(本小题满分12分) 如图,在五面体ABCDE中,EA=ED=EC=2,且EA、ED、EC 两两垂直,AB∥CE,AB=1,F为CD中点 (1)求证:BF∥平面ADE (2)判断EF与面BCD能否垂直,证明你的结论。
19.(本小题满分12分) 试题详情
已知椭圆C:x2+ ,直线 ,直线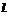 :y=mx+1 :y=mx+1 试题详情
(1)求证:当m∈R时,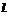 与C恒有两个不同交点; 与C恒有两个不同交点; 试题详情
(2)设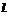 交C于A、B两点,求AB中点M的轨迹。 交C于A、B两点,求AB中点M的轨迹。
20.(本小题满分14分) 试题详情
在x轴上有一质点M从原点出发,每次都沿x轴的正方向移动一个或两个单位,其中向右移动一个单位的概率为 ,移动两个单位的概率为 ,移动两个单位的概率为 ,设M移动到(n,0)的概率为Pn ,设M移动到(n,0)的概率为Pn (1)求P1、P2、P3; 试题详情
(2)若Pn+2= Pn+1+ Pn+1+ Pn问数列{Pn+2-Pn+1}为等差数列还是等比数列或者都不是?说明理由。 Pn问数列{Pn+2-Pn+1}为等差数列还是等比数列或者都不是?说明理由。 (3)求数列{Pn}的通项公式。
21.(本小题满分14分) 试题详情
f(x)=4x+ax2- x3在[-1,1]上是增函数 x3在[-1,1]上是增函数 (1)求实数a的值组成的集合A; 试题详情
(2)设关于x的方程f(x)=2x+ x3两非零实根为x1,x2,试问:是否存在实数m使不等式m2+tm+1≥|x1-x2|对于任意a∈A及t∈[-1,1]恒成立,若存在求出m取值范围,若不存在,说明理由。 x3两非零实根为x1,x2,试问:是否存在实数m使不等式m2+tm+1≥|x1-x2|对于任意a∈A及t∈[-1,1]恒成立,若存在求出m取值范围,若不存在,说明理由。 A.△ABC内接于⊙O,AB=AC,直线MN切⊙O于C, 弦BD∥MN,AC、BD交于点E (1)求证:△ABE≌△ACD (2)AB=6,BC=4,求AE 试题详情
 四、选考题(10分,请从所给的三道题中任选一道作答,并用2B铅笔在答题卡上把所选对应题目的题号涂黑) 四、选考题(10分,请从所给的三道题中任选一道作答,并用2B铅笔在答题卡上把所选对应题目的题号涂黑)
B.求点P(2,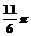 )到直线 )到直线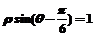 的距离。 的距离。 试题详情
C.已知a,b,c,d都是实数,且a2+b2=1,c2+d2=1,求证:|ac+bd|≤1. 试题详情
一、选择题:(每小题5分,共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A B D D D A A D B B C 二、填空题(每小题4分,共16分) 13.90° 14. m< 且m≠- 且m≠- 15.
12 16. 15.
12 16.  三、解答题 17.(12分) (3分)
(3分)
sin sin sin +cos +cos cos cos = = (6分)
(6分)
cos( - - )= )= (8分)
(8分)
 (10分) (10分)
∴sin( - - )=- )=- (12分)
(12分) 18.(12分) (1)略
(6分) (2)不垂直
(12分)  方法一:求出EF= 方法一:求出EF= ,BE= ,BE= ,取EC中点G,BG=2,GF=1,BF= ,取EC中点G,BG=2,GF=1,BF=
∴△BEF是等腰三角形 ∴EF与BF不垂直 ∴EF与平面BDC不垂直。 方法二:向量法,如图建立坐标系 E(0,0,0),F(1,1,0),B(0,1,2),C(0,2,0)  =(1,1,0), =(1,1,0), =(0,1,2) =(0,1,2)  ∴EF与BC不垂直 ∴EF与平面BDC不垂直。 19.(12分) (1)方法一:直线亘这定点P(0,1)
(2分) 而P(0,1)在椭圆C内
(3分)
∴ 与C恒有两个不同交点 (4分) 与C恒有两个不同交点 (4分) 方法二:由 (2分)
(2分)
△=(2m)2+4×3×(4+m2)>0
(3分)
∴ 与C恒有两个不同交点
(4分) 与C恒有两个不同交点
(4分) (2)方法一:设A(x1,y1),B(x2,y2),M(x,y)则
 (6分) (6分)
 x1+x2+ x1+x2+ =0(∵x1≠x2) =0(∵x1≠x2)
x1+x2=2x,y1+y2=2y,k=m
(8分)
∴x+ m=0
(9分) m=0
(9分)
又y=mx+1
(10分) 消去m得4x2+(y- )2= )2= (12分)
(12分) ∴M点轨迹方程为4x2+y2-y=0(y≠0) 方法二:由 (4+m2)x2+2mx-3=0 (4+m2)x2+2mx-3=0
 (10分) (10分)
消去m得4x2+y2-y=0(y≠0) ∴M点轨迹方程为4x2+y2-y=0(y≠0)
(12分) 20.(14分) (理)(1)P1= ,P2= ,P2= ,P3= ,P3= (2)Pn+2-Pn+1= ∴ ∴{Pn+2-Pn+1}是公比为- 的等比数列
(10分) 的等比数列
(10分) (3)
Pn+2-Pn+1=(P2-P1)?(- )n-1=(- )n-1=(- )n+1 )n+1 P2-P1=(- )2,P3-P2=(- )2,P3-P2=(- )3,……,Pn-Pn-1=(- )3,……,Pn-Pn-1=(- )n )n 相加:Pn-P1=(- )2+(- )2+(- )3+…+(- )3+…+(- )n= )n= [1-(- [1-(- )n-1] )n-1] ∴Pn= (14分)
(14分) (文)(1)an= (4分) (4分) b1=a1=2,b2= ,q= ,q= bn=b1qn-1=2?( )n-1
(7分) )n-1
(7分) (2)Cn= (8分)
(8分) Tn=1+3?41+5?42+……+(2n-1)?4n-1 4Tn=4+3?42+5?43+……+(2n-1)?4n -3Tn=1+2?41+2?42+……+2?4n-1 -(2n-1)?4n =- [(6n-5)4n+5] [(6n-5)4n+5] ∴Tn= [(6n-5)4n+5] [(6n-5)4n+5] 21.(14分) (理)(1)f′(x)=4+2ax-2x2,由题意f′(x)≥0在[-1,1]上恒成立 (2分) ∴ ∴A=[-1,1]
(5分) ∴A=[-1,1]
(5分) (2)方程f(x)=2x+ x3可化为x(x2-ax-2)=0 x3可化为x(x2-ax-2)=0 ∵x1≠x2≠0, ∴x1,x2是x2-ax-2=0两根
(7分) △=a2+8>0,x1+x2=a,x1x2=2 ∴|x1-x2|= ∵-1≤a≤1 ∴|x1-x2|最大值是 (10分) (10分) ∴m2+tm+1≥3在t∈[-1,1]上恒成立 令g(t)=mt+t2-2 ∴ m≥2或m≤-2
(14分) 故存在m值,其取值范围为(-∞,-2]∪[2,+∞) (文)(1)f′(x)=3x2+b 由已知f′(x)在[-1,1]上恒成立
(3分) ∴b≥-3x2在[-1,1] 上恒成立 ∵-3x2在[-1,1]上最大值为0
(6分) ∴b≥0
(7分) (2)f(x)在[-1,1]上最大值为f(1)=1+b (9分) ∴b2-tb+1≥1+b
(10分) 即b2-(t+1)b≥0恒成立,由b≥0得 ∴b-(t+1)≥0,t+1≤b恒成立 ∴t≤-1
(14分) 四、选考题:(10分) A.(1) △ABE≌△ACD (5分) △ABE≌△ACD (5分) (2) △ABC∽△BEC △ABC∽△BEC ∴ (8分)
(8分) ∴AE= (10分)
(10分) B.P(2, )
P( )
P( ) (3分) ) (3分)  x- x- y+2=0 (7分) y+2=0 (7分) D= (10分)
(10分) C.设a=cos ,b=sin ,b=sin ,c=cos ,c=cos ,d=sin ,d=sin (4分)
(4分) |ac+bd|=|cos cos cos +sin +sin sin sin |
(6分) |
(6分)
=|cos( - - )|≤1
(10分) )|≤1
(10分) 方法二:只需证(ac+bd)2≤(a2+b2)(c2+d2)
(6分) 即证:2abcd≤a2d2+b2c2
(8分) 即证:(ad-bc)2≥0 上式显然成立 ∴原不等式成立。
(10分)
| 
 的定义域为( )
的定义域为( ) } B.(
} B.( ,+∞) C.(-∞,
,+∞) C.(-∞, ) D.[
) D.[ ,+∞]
,+∞] C.y=2x D.y=-2x3
C.y=2x D.y=-2x3 )-sin2(2x+
)-sin2(2x+ )的最小正周期是( )
)的最小正周期是( ) B.
B. C.4
C.4 D.
D.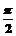
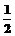 ,-5 D.-
,-5 D.-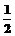 ,-11
,-11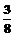 B.
B.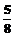 C.
C.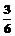 D.
D.
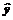 =0.5x-85中,变量x=200时,变量y的值一定是15
=0.5x-85中,变量x=200时,变量y的值一定是15 是两条不重合的直线,
是两条不重合的直线,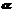 、
、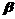 是两个不重合的平面,给出下列四个命题:①若
是两个不重合的平面,给出下列四个命题:①若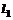
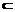
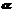 ,
,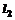
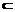
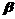 ,
,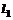 ∥
∥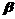 ,
,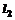 ∥
∥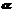 ,则
,则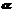 ∥
∥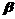 ②
②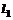 ⊥
⊥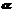 ,
,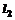 ⊥
⊥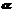 ,则
,则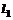 ∥
∥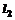 ③若
③若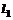 ⊥
⊥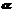 ,
,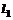 ⊥
⊥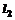 ,则
,则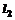 ∥
∥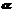 ④若
④若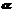 ⊥
⊥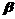 ,
,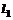
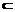
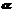 ,则
,则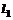 ⊥
⊥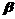 ,其中正确的命题个数为( )
,其中正确的命题个数为( )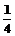
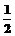
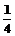
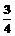
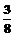

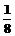 B.
B.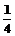 1
1