注 意 事 项
考生在答题前请认真阅读注意事项及各题要求
1.
本试卷共4页,包含选择题(第1题~第10题)、填空题(第11题~第16题)、解答题(第17题~21题)三部分.本次考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.
2.
答题前,请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔写在试卷及答题卡上的指定位置.
3.
作答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其它位置作答一律无效.作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其它答案.
4.
如有作图需要,可用2B铅笔作答,并请加黑加粗,描写清楚.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么 次独立重复试验中恰好发生
次独立重复试验中恰好发生 次的概率
次的概率
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,恰有一项是符合题目要求的,请把正确答案填涂在答题卡的指定位置。
1.已知集合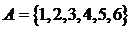 ,
,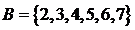 ,则集合
,则集合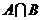 的真子集个数为 ( )
的真子集个数为 ( )
A 32个 B 31个 C 64个
D 63个
试题详情
2.已知条件p: 内是增函数,条件q:
内是增函数,条件q: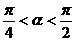 ,则p是q成立的( )
,则p是q成立的( )
A
充要条件 B
充分不必要条件
C
必要不充分条件 D
既不充分又不必要条件
试题详情
试题详情
试题详情
4.下列命题正确的是 ( )
A
垂直于同一平面的两个平面互相平行
试题详情
B
经过平面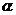 的一条斜线的平面
的一条斜线的平面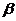 与平面
与平面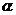 一定不垂直
一定不垂直
C
若a,b是异面直线,则过直线a一定不能作与直线b垂直的平面
试题详情
试题详情
试题详情
试题详情
6.已知二项式(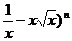 的展开式中含有
的展开式中含有 的项, 则n的一个可能值是
( )
的项, 则n的一个可能值是
( )
A 6 B
9 C
8 D
10
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
二、填空题:本大题共6小题,每小题5分,共30分.请将答案填写在答题卡的指定位置.
11.将一组样本数据中的每一个数据都乘以2,再都减去80,得到一组新的样本数据. 若求得新的样本数据的平均数是1.2,方差是4.4,则原样本数据的平均数为 ▲ ,方差为 ▲ 。
试题详情
试题详情
试题详情
试题详情
试题详情
15.如图为类似课本研究性学习课题《杨辉三角》中的竖直平面内一些通道,
图中粗线条均表示通道,一钢珠从入口处自上而下沿通道自由落入乙处
的概率是 ▲ 。
(第15题图)
试题详情
16.已知直线 相切,其中m、
相切,其中m、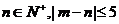 ,试写出所有满足条件的有序实数对(m,n): ▲ 。
,试写出所有满足条件的有序实数对(m,n): ▲ 。
试题详情
三、解答题:本大题共5小题,共70分. 解答应写出文字说明,证明过程或演算步骤。请将解题过程写在答题卡指定的方框内。
试题详情
已知△ABC的面积为 ,且满足
,且满足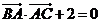 。
。
试题详情
(Ⅰ)求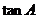 的值;
的值;
试题详情
(Ⅱ)求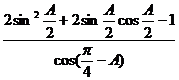 的值。
的值。
试题详情
试题详情
试题详情
(Ⅰ)求椭圆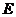 的方程;
的方程;
试题详情
试题详情
试题详情
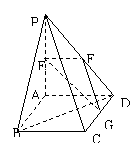 如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
|
试题详情
(Ⅲ)在线段CD上是否存在一点Q,使得A点到平面EFQ的距离为0.8,若存在,求出CQ的值;若不存在,请说明理由。 试题详情
试题详情
已知 ,函数 ,函数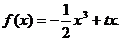 试题详情
(Ⅰ)当t=1时,求函数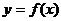 在区间[0,2]的最值; 在区间[0,2]的最值; 试题详情
(Ⅱ)若 在区间[-2,2]上是单调函数,求t的取值范围; 在区间[-2,2]上是单调函数,求t的取值范围; 试题详情
(Ⅲ))是否存在常数t,使得任意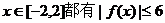 恒成立,若存在,请求出t,若不存在请说明理由. 恒成立,若存在,请求出t,若不存在请说明理由. 试题详情
试题详情
设集合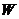 是满足下列两个条件的无穷数列 是满足下列两个条件的无穷数列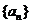 的集合: 的集合: 试题详情
试题详情
试题详情
试题详情
(Ⅲ))设数列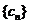 的各项均为正整数,且 的各项均为正整数,且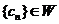 ,试证 ,试证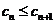 。 。 命题:周志国 冯建国 审校:冯建国 刘兴东 刘其鹿 淮安市2006-2007学年度高三年级第四次调查测试 试题详情
说明: 一、本解答给出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。 二、对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定后续部分的给分,但不得超过该部分正确解答所给分数的一半;如果后续部分的解答存在较严重的错误,则不再给分。 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。 四、每题只给整数分数,选择题和填空题不给中间分。 一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案 B C C D A A B C B D 二、填空题: 11.40.6,1.1 12. 13. 13. 14.30 15. 14.30 15.  16.(1,1),(2,2),(3,4),(4,8) 16.(1,1),(2,2),(3,4),(4,8) 三、解答题: 17.(Ⅰ) , ①
…………………2分 , ①
…………………2分 又 , ∴ , ∴ ②
……………… 4分 ②
……………… 4分 由①、②得 …………………………………………………………… 6分
…………………………………………………………… 6分 (Ⅱ)  ……………………………………… 8分 ……………………………………… 8分  …………………………………………………………………… 10分 …………………………………………………………………… 10分   …………………………………………………………………………12分 …………………………………………………………………………12分 18.(Ⅰ)设点  ,则 ,则 , ,  , ,
 ,又 ,又 , ,
 ,∴椭圆的方程为: ,∴椭圆的方程为: …………………………………………7分 …………………………………………7分
(Ⅱ)当过 直线 直线 的斜率不存在时,点 的斜率不存在时,点 ,则 ,则 ; ; 当过 直线 直线 的斜率存在时,设斜率为 的斜率存在时,设斜率为 ,则直线 ,则直线 的方程为 的方程为 , , 设 ,由 ,由 得: 得:  …………………………………………10分 …………………………………………10分

 ……13分
……13分
综合以上情形,得: ……………………………………………………14分 ……………………………………………………14分

∴GH∥AD∥EF,∴E,F,G,H四点共面. ……………………1分 又H为AB中点,∴EH∥PB. 又EH 面EFG,PB 面EFG,PB 平面EFG, 平面EFG, ∴PB∥平面EFG.
………………………………4分 (Ⅱ)取BC的中点M,连结GM、AM、EM,则GM//BD, ∴∠EGM(或其补角)就是异面直线EG与BD所成的角.……6分 在Rt△MAE中,  , , 同理 ,又GM= ,又GM= ,………………7分 ,………………7分 ∴在△MGE中, ………………8分
………………8分 故异面直线EG与BD所成的角为arccos ,
………………………………9分 ,
………………………………9分

又AB∩PA=A,∴AD⊥平面PAB. ……………………………………10分 又∵E,F分别是PA,PD中点,∴EF∥AD,∴EF⊥平面PAB. 又EF 面EFQ,∴面EFQ⊥面PAB. ………………………………11分 面EFQ,∴面EFQ⊥面PAB. ………………………………11分 过A作AT⊥ER于T,则AT⊥平面EFQ, ∴AT就是点A到平面EFQ的距离. ………………………………12分 设 ,则 ,则 在 ,
…………………………13分 ,
…………………………13分 解得 故存在点Q,当CQ= 故存在点Q,当CQ= 时,点A到平面EFQ的距离为0.8. ……………………… 14分 时,点A到平面EFQ的距离为0.8. ……………………… 14分 解法二:建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
| | | | | |
