
2006年贵州省贵阳市初中学业考试试卷(课改区)
一.选择题:(以下每小题均为A、B、C、D四个选项,其中只有一个选项正确,请把正确选项的字母选入该题的括号内,每小题4分,共20分)
1.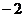 的绝对值等于
( )
的绝对值等于
( )
(A) 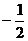 (B)
(B) 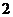 (C)
(C)
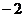 (D)
(D) 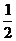
2.用计算器计算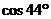 的结果(精确到0.01)是
( )
的结果(精确到0.01)是
( )
(A) 0.90 (B) 0.72 (C) 0.69 (D) 0.66
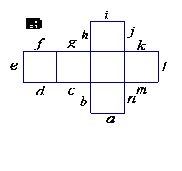
3.以下适合普查的是 ( )
(A)了解一批灯泡的使用寿命 (B)调查全国八年级学生的视力情况
 (C)评价一个班级升学考试的成绩 (D)了解贵州省的家庭人均收入
(C)评价一个班级升学考试的成绩 (D)了解贵州省的家庭人均收入
4.图1是正方体的一个平面展开图,如果折叠成原
来的正方体时与边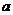 重合的是
( )
重合的是
( )
(A) 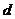 (B)
(B) 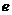
(C) 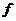 (D)
(D) 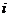
5.小明根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还。”如果用纵轴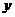 表示父亲与儿子行进中离家的距离,用横轴
表示父亲与儿子行进中离家的距离,用横轴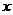 表示父亲离家的时间,那么下面的图象与上述诗的含义大致吻合的是
( )
表示父亲离家的时间,那么下面的图象与上述诗的含义大致吻合的是
( )
二.填空题:(每小题3分共30分)
6.

 7.分解因式:
7.分解因式: ;
;
8.如图2,P为ㄓABC中BC边的延长线上一点,
9.掷一枚质地均匀的小正方体,它的六个面上分别
标有1、2、3、4、5、6,则朝上一面的数字是奇数
的概率是 ;
10.已知点A(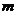 ,2)在双曲线
,2)在双曲线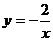 上,则
上,则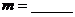 ;
;
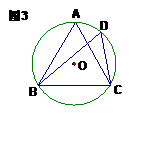
11.如图3,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC = ;
12.在一节综合实践课上,六名同学做手工的数量(单位:件)分别是:5,7,3,6,6,4;
则这组数据的中位数为 件;
13.如她4,B是线段AC上的一点,且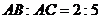 ,分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为
;
,分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为
;
15.如图6,这是一个供滑板爱好者使用的U型池,该U型池
可以看作是一个长方体去掉一个“半圆柱”而成,中间可
供滑行部分的截面是半径为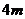 的半圆,其边缘AB = CD =
的半圆,其边缘AB = CD =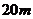 ,
,
点E在CD上,CE =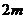 ,一滑板爱好者从A点滑到E点,则
,一滑板爱好者从A点滑到E点,则
他滑行的最短距离约为
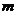 ;(边缘部分的厚度忽略不极,结果保留整数)
;(边缘部分的厚度忽略不极,结果保留整数)
三.解答题:
16.(本题满分6分)已知二元一次方程:(1)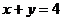 ;(2)
;(2)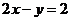 ;(3)
;(3)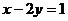 ;
;
请从这三个方程中选择你喜欢的两个方程,组成一个方程组,并求出这方程组的解;
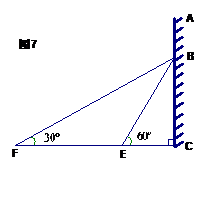 18.(本题满分10分)如图7 ,在某建筑物AC上,挂着“多彩贵州”的宣传条幅BC,小明站在点F处,看条幅顶端B,测的仰角为
18.(本题满分10分)如图7 ,在某建筑物AC上,挂着“多彩贵州”的宣传条幅BC,小明站在点F处,看条幅顶端B,测的仰角为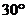 ,再往条幅方向前行
,再往条幅方向前行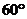 ,求宣传条幅BC的长,(小明的身高不计,结果精确到
,求宣传条幅BC的长,(小明的身高不计,结果精确到
19.(本题满分10分)桌面上放有4张卡片,正面分别标有数字1,2,3,4,这些卡片除数字外完全相同,把这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出一张,记下卡片上的数字后仍放反面朝上放回洗匀,乙从中任意抽出一张,记下卡片上的数字,然后将这两数相加;
(1)请用列表或画树状图的方法求两数和为5的概率;(6分)
(2)若甲与乙按上述方式作游戏,当两数之和为5时,甲胜;反之则乙胜;若甲胜一次得12分,那么乙胜一次得多少分,这个游戏对双方公平吗?
20.(本题满分10分)甲乙两人加工同一种玩具,甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等,已知甲乙两人每天共加工35个玩具,求甲乙两人每天各加工多少个玩具?
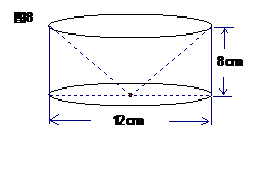
21.(本题满分10分)如图8,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB =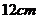 ,高BC =
,高BC =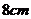 ,求这个零件的表面积;(结果保留
,求这个零件的表面积;(结果保留 )
)
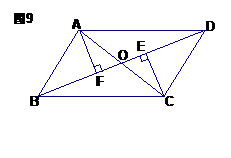
22.(本题满分10分)如图9,在平行四边形ABCD中,对角线AC\BD相交于点O,AF⊥BD,CE⊥BD,垂足分别为E、F;
(1)连结AE、CF,得四边形AFCE,试判断四边形AFCE是下列图形中的哪一种?
①平行四边形;②菱形;③矩形;
(2)请证明你的结论;
23.(本题满分12分)某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元;
(1)符合公司要求的购买方案有几种?请说明理由;(8分)
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金不低于1500元,那么应选择以上那种购买方案?(4分)
24.(本题满分10分)两条平行直线上各有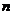 个点,用这
个点,用这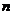 对点按如下的规则连接线段;
对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
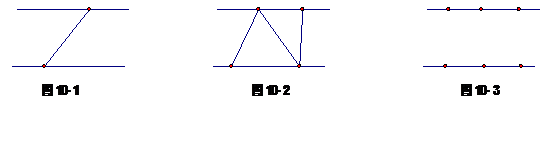
图10-1展示了当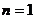 时的情况,此时图中三角形的个数为0;
时的情况,此时图中三角形的个数为0;
图10-2展示了当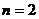 时的一种情况,此时图中三角形的个数为2;
时的一种情况,此时图中三角形的个数为2;
(1)当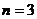 时,请在图10-3中画出使三角形个数最少的图形,此时图中三角形的个数为
时,请在图10-3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;(5分)
(2)试猜想当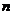 对点时,按上述规则画出的图形中,最少有多少个三角形?(3分)
对点时,按上述规则画出的图形中,最少有多少个三角形?(3分)
(3)当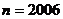 时,按上述规则画出的图形中,最少有多少个三角形?(2分)
时,按上述规则画出的图形中,最少有多少个三角形?(2分)
25.(本题满分12分)某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个;
(1)假设销售单价提高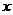 元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个;(用含
元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个;(用含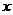 的代数式表示)(4分)
的代数式表示)(4分)
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请求出最大利润,此时篮球的售价应定为多少元?(8分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com