
2006--2007学年度九年级第一学期期末考试试卷
(时间:90分钟 满分:120分)
一、选择题(每小题4分,共40分,只有一个答案正确)
1.一个不透明的封闭容器中,装着8个黑球和3个白球,摸到白球的概率为p,则p的值为
A.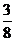 B.
B.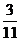 C.
C.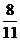 D.
D.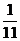
2.下列说法中错误的个数是
①经过旋转,图形上任意两点的连线与其对应两点的连线相等;
②经过旋转,图形上每一点到旋转中心的距离相等;
③经过旋转,图形上每一点转动的角度都相等;
④经过旋转,图形上可能存在不动点;
⑤把一个图形绕着某一点旋转一定的角度,它仍能与原图形重合,那么说这两个图形关于这点对称或中心对称;
⑥一个图形是中心对称图形,那它一定不是轴对称图形;
A.1 B.
3.点P(12,5)关于原点的对称点是Q,则线段PQ的长度是
A.12 B.
4.抛物线y=3(z+4)(z-3)与z轴,y轴的交点坐标分别为
A.(-4,0),(3,O),(0,-12) B.(4,O),(-3,O),(O,12)
C.(-4,O),(3,0),(O,-36) D.(4,0),(-3,0),(O,36)
5.已知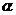 为锐角,且sin(90°-
为锐角,且sin(90°-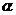 )=
)=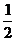 ,则
,则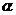 的度数是
的度数是
A.30° B.45° C.60° D.90°
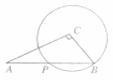
6.如图所示,AB是⊙O的直径,BC是⊙O的切线,AC交⊙O于D,AB=6,BC=8,则tan∠DBC等于
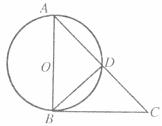
A.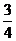 B.
B.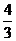 C.
C.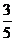 D.
D.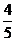
7.已知两圆的圆心距为6,两圆的半径分别是方程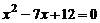 的两个根,那么两个圆的位置关系是
的两个根,那么两个圆的位置关系是
A.相交 B.外离 C.内切 D.外切
8.如图,两块完全重合的正方形纸片,如果上面的一块绕正方形的中心O做0°~90°的旋转,那么旋转时露出的△ABC的面积(s)随着旋转角度(n)的变化而变化,下面表示S与n的关系的图像大致是
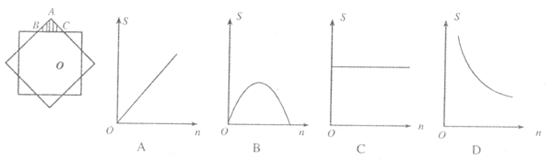
9.如图,EF∥GH∥MN∥BC,则图中共有多少对相似三角形
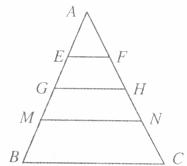
A.4 B.
10.下列命题中,错误命题的个数是
①一个锐角的正切值一定不大于1;
②垂直于半径的直线是圆的切线;
③平分弦(不是直径)的直径垂直于这条弦;
④位似图形对应顶点的连线相交于一点且对应边互相平行
A.1
B.
二、填空题(每小题4分,共32分)
11.我们家中的电风扇叶片可以看作是一个旋转的对称图形,电风扇叶片至少旋转 度 能与自身重合。

12.如上图所示,OA、OB、OC、OD两两不相交,且半径都是
13.抛物线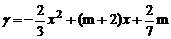 的对称轴为直线
的对称轴为直线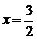 ,则m的值为
。
,则m的值为
。
14.已知△ABC∽△A’B’C’,若△ABC的三边分别为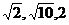 ,△A’B’C’的两边长分别为
,△A’B’C’的两边长分别为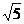 和1,则△A’B’C’的第三边长为 。
和1,则△A’B’C’的第三边长为 。
15.在Rt△ABC中,一锐角的正切值为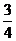 ,其周长是24,则三边长分别为 。
,其周长是24,则三边长分别为 。
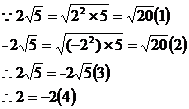
以上推理过程中的错误出现在第 步(填序号)。
17.若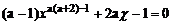 是关于x的一元二次方程,则a的值是 。
是关于x的一元二次方程,则a的值是 。
18.观察下列各式:2×4=32-l;3×5=42-1;4×6=52-l;…;10×12=ll2-1,…将你猜想的规律用只含一个字母的式子,表示出来 。
三、解答题(19―22小题,每题7分,23题8分,24题12分,共48分)
19.(7分)小强十分喜欢饲养小家兔,在集市上买了一张
(1)设矩形的一边长为x(m),面积y(m2),求y关于x的函数关系式,并写出自变量x的取值范围。
(2)当x为何值时,所围的养兔场使兔子的活动区域最大?最大面积是多少?
20.(7分)如图,在直角坐标系中,以x轴上一点P(1,0)为圆心的圆与x轴、y轴分别交于A、B、C、D四点,C点的坐标为(0,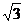 )。
)。

(1)写出A、B、D点的坐标。
(2)若抛物线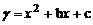 过A、D两点,求这条抛物线的解析式,并判断点B是否在所求的抛物线上,说明理由。
过A、D两点,求这条抛物线的解析式,并判断点B是否在所求的抛物线上,说明理由。
21.(7分)在新城区建设中,要拆除一废旧的水塔,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在从离B点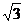 ≈1.732,
≈1.732,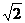 ≈1.414)
≈1.414)
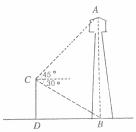
22.(7分)在图中“配紫色”游戏中,“配紫色”成功的概率是多少?(红色与蓝色可配成紫色)

游戏规则:
1.分别从A、B中各拿出一种颜色配成一种新颜色;
2.不能单独从A或B中配颜色;
23.如图,已知Rt△ABC中,∠C=90°,AC=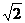 ,BC=1,若以C为圆心,CB为半径的圆交AB于P,则AP等于多少?
,BC=1,若以C为圆心,CB为半径的圆交AB于P,则AP等于多少?
24.(12分)我们使用的教科书第54页《观察与猜想》的题目是:发现一元二次方程根与系数的关系,其中有这样一段话:“……通过上面的观察可以猜想:对于任意一元二次方程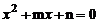 (m,n是系数),方程的两个根
(m,n是系数),方程的两个根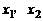 和系数m,n可能有如下关系:
和系数m,n可能有如下关系:
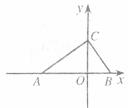
如图,在平面直角坐标系内,Rt△ABC的斜边AB在x轴上,点C的坐标为(O,6),AB=15,∠CBA>∠CAB,且tan∠CAB,tan∠CBA是关于x的方程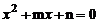 的两根。
的两根。
(1)求m,n的值。
(2)若∠ACB的平分线交x轴于D,求直线CD的解析式。
(3)在(2)的条件下,直线CD上是否存在点M,过M点作BC的平行线,交y轴于N,使以M、N、B、C为顶点的四边形是平行四边形,若存在,请直接写出M点的坐标;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com