1．-3的相反数是

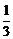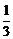   A．-3             B．-              C．            D．3

2．第29届北京奥运会火炬接力活动历时130天,传递行程约为137000km．用科学记数法表示137000km是

A．1.37×10⁵km    B．13.7×10⁴km       C．1.37×10⁴km    D．1.37×10³km

3．若分式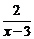有意义．则x应满足的条件是

   A．x≠0           B．x≥3             C．x≠3           D．x≤3

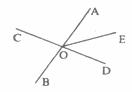
4．如下图,直线AB、CD相交于点O．OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是

  A．40°           B．50°               C．80°          D． 100°

5．下列各式中，正确的是

     A．2< <3    B．3<<4        C．4<<5     D． 14<<16

6．下列计算正确的是

    A．a²+a²=a⁴    B．a⁵?a²=a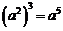⁷    C．   D．2a²-a²=2

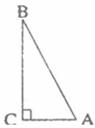
7．如下图,在Rt△ABC中，∠C=90°,AC=1,BC=2．以边BC所在直线为轴，把△ABC旋转一周,得到的几何体的侧面积是

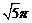     A．       B．2        C．          D．2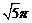    

8．如图所示的几何体的俯视图是

9．下列调查方式中．不合适的是

A．了解2008年5月18日晚中央也视台“爱的奉献”抗震救灾文艺晚会的收视率,采用抽查的方式

B．了解某渔场中青鱼的平均重量,采用抽查的方式

 C．了解某型号联想电脑的使用寿命，采用普查的方式

    D．了解一批汽车的刹车性能，采用普查的方式

10．一盘蚊香长l00cm，点燃时每小时缩短10cm,小明在蚊香点燃5h后将它熄灭，过了2h,他再次点燃了蚊香．下列四个图象中，大致能表示蚊香剩余长度y(cm)与所经过时间t(h)之间的函数关系的是 

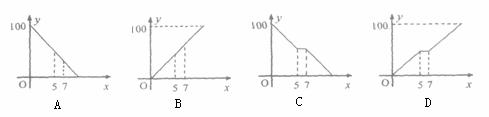
第Ⅱ卷  (非选择题   共120分)

11．分解因式：a²-4=______________

12．已知⊙O₁与⊙O₂的半径分别为2cm和3cm，当⊙O₁与⊙O₂外切时，圆心距O₁O₂=______

13．如下图，请填写一个适当的条件：___________,使得DE∥AB.

14．小华在解一元二次方程x²-4x=0时．只得出一个根是x=4,则被他漏掉的一个根是x=____．

15．小明上学期六门科目的期末考试成绩(单位：分)分别是：120，115，x，60，85,80．若平均分是93分，则x=_________．

16．如图，点O（0，0)，B(0，1)是正方形OBB₁C的两个顶点，以对角线OB₁为一边作正方形OB₁B₂C₁，再以正方形OB₁B₂C₁的对角线OB₂为一边作正方形OB ₂B₃C ₁，……，依次下去．则 点B ₆的坐标是________________．

17(本小题6分)

计算

18．(本小题6分)

先化简，再求值：其中x=-1,y=.

19．(本小题6分)

解不等式3x-2<7,将解集在数轴上表示出来,并写出它的正整数解．

20．(本小题8分)

    一只不透明的袋子中装有6个小球,分别标有l、2、3；、4、5、6这6个号码，这些球除号码外都相同．

    (1)直接写出事件“从袋中任意摸出一个球，号码为3的整数倍”的概率P₁；

    (2)用画树状图或列表格等方法，求事件“从袋中同时摸出两个球,号码之和为6”的概率P₂．

21．(本小题8分)

某县教育部门对该县参加奥运知识竞赛的7500名初中学生的初试成绩(成绩均为整数)进行一次抽样调查，所得数据如下表：

成绩分组

60.5～70.5

70.5～80.5

80.5～90.5

90.5～100.5

频数

50

150

200

100

(1)抽取样本的容量为___________；

    (2)根据表中数据,补全图中频数分布直方图；

    (3)样本的中位数所在的分数段范围为                ；

    (4)若规定初试成绩在90分以上(不包括90分)的学生进入决赛，则全县进入决赛的学生约为    人．

22．(本小题8分)

    某民营企业为支援四川地震灾区，特生产A、B两种型号的帐篷．若A型帐篷每顶需篷布60平方米,钢管48米；B型帐篷每顶需篷布125平方米，钢管80米．该企业在生产这批帐篷时恰好(不计损耗)用了篷布9900平方米，钢管6720米．问：该企业生产了A、B两种型号的帐篷各多少顶?

23．(本小题8分)

如图所示的网格中有A、B、C三点．

    (1)请你以网格线所在直线为坐标轴建立平面直角坐标系,使A、B两点的坐标分别为A(2，-4)、 B(4，-2)，则C点的坐标是_____________；

    (2)连结AB、BC、CA，先以坐标原点O为位似中心,按比例尺1：2在y轴的左侧画出△ABC缩小后的△，再写出点C对应点的坐标 

24．(本小题9分)

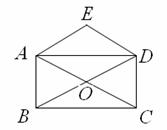
已知；如下图．矩形ABCD的对角线AC与BD相交于点O，点O关于直线AD的对称点是E，连结AE、DE．

    (1)试判断四边形AODE的形状,不必说明理由；

    (2)请你连结EB、EC．并证明EB=EC．  

25．(本小题9分)

    某项工程需要沙石料2×l0⁶立方米，阳光公司承担了该工程运送沙石料的任务．

    (1)在这项任务中平均每天的工作量v(立方米／天)与完成任务所需要的时间t(天)之间具有怎样的函数关系?写出这个函数关系式．

    (2)阳光公司计划投入A型卡车200辆，每天一共可以运送沙石料2×10⁴立方米，则完成全部运送任务需要多少天?如果工作了25天后，由于工程进度的需要，公司准备再投入A型卡车120辆,在保持每辆车每天工作量不变的前提下，问：是否能提前28天完成任务?

26．(本小题10分)

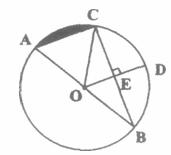
如下图，AB是⊙O的直径,BC是⊙O的弦，半径OD⊥BC,垂足为E，若BC=6，DE=3．

求：(1) ⊙O的半径；

  (2)弦AC的长；

  (3)阴影部分的面积．

27．(本小题l0分)

    我们约定,若一个三角形(记为△A₁)是由另一个三角形(记为△A)通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A₁是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图l是由△A复制出△A₁，又由△A_l复制出△A₂，再由△A₂复制出△A₃，形成了一个大三角形，记作△B.以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠．

    (1)图l中标出的是一种可能的复制结果．它用到_____次平移．_______次旋转．小明发现△B∽△A，其相似比为_________．若由复制形成的△C的一条边上有11个小三角形(指有一条边在该边上的小三角形)，则△C中含有______个小三角形；

    (2)若△A是正三角形，你认为通过复制能形成的正多边形是________；

    (3)在复制形成四边形的过程中，小明用到了两次平移一次旋转，你能用两次旋转一次平移复制形成一个四边形吗?如果能，请在图2的方框内画出草图，并仿照图1做出标记；如果不能,请说明理由；

(4)图3是正五边形EFGHI．其中心是O．连结O点与各顶点．将其中的一个三角形记为 △A，小明认为正五边形EFGHI是由复制形成的一种结果，你认为他的说法对吗?请判断并说明理由．

28．(本小题14分)

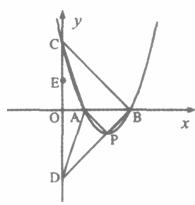
    如图所示，在平面直角坐标系中．二次函数y=a(x-2)²-1图象的顶点为P，与x轴交点为 A、B，与y轴交点为C．连结BP并延长交y轴于点D.

    (1)写出点P的坐标；

    (2)连结AP，如果△APB为等腰直角三角形，求a的值及点C、D的坐标；

    (3)在(2)的条件下，连结BC、AC、AD，点E(0，b)在线段CD(端点C、D除外)上,将△BCD绕点E逆时针方向旋转90°，得到一个新三角形．设该三角形与△ACD重叠部分的面积为S，根据不同情况，分别用含b的代数式表示S．选择其中一种情况给出解答过程，其它情况直接写出结果；判断当b为何值时,重叠部分的面积最大?写出最大值．