
2008年潍坊市诸城九年级练习
数学试卷
一、选择题(本大题共12小题,每小题3分,共36分)每小题都给出代号为(A)、(B)、(C)、(D)的四个结论。其中只有一个是正确的,选择正确结论的代号填在括号内。
1.实数a,b在数轴上的位置如图所示,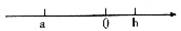 则下列各式正确的 是( )
则下列各式正确的 是( )
A.a>b B.a>-b C.a<b D.-a<-b
2.在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为4.6×108帕的钢材,那么4.6×108的原数为( )
A.4 600 000 B.46 000
3.如图,AB//CD,∠1=110°∠ECD=70°,∠E的大小是( )

A.30° B.40° C.50° D.60°
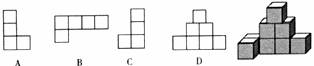
4.下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的主视图是( )
5.国家实行一系列“三农”优惠政策后,农民收入大幅度增加,下图是我省2001年至2006年农村居民人均年收入统计图,则这6年中农村居民人均年收入的中位数是( )

A.5132 B.
6.如图,在菱形ABCD中,对角线AC,BD分别等于8和6,将BD沿CB的方向平移,使D与A重合,B与GB延长线上的点E重合,则四边形AECD的面积等于( )

A.36 B.
7.王英同学从A地沿北偏西60°方向走
A.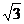 m B.100 m C.150m D.100
m B.100 m C.150m D.100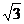 m
m
8.如图,△ABC内接于⊙O,∠C=30°,AB=2,则⊙O的半径为( )

A.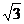 B.2 C.2
B.2 C.2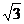 D.4
D.4
9.有一边长为2的正方形纸片ABCD,先将正方形ABCD对折,设折痕为EF(如图(3));再沿过点D的折痕将角A反折,使得点A落在EF的H上(如图(4)),折痕交AE于点G,则EG的长度为( )
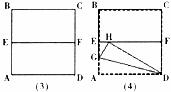
A. B.
B. C.
C.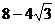 D.
D.
10.“五一”放假期间,某校八年级学生小明骑自行车到30千米的国家环境保护区进行“社会小调查”活动,小明出发30分钟后,小亮乘汽车出发,结果他们同时到达,已知汽车速度是自行车速度的2倍。若设汽车速度为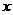 千米/小时,则小明到达目的地用了(
)
千米/小时,则小明到达目的地用了(
)
A.2小时 B.1.5小时 C.1小时 D.45分钟
11.如图,在△ABC中,AB=AC=2,∠BAC=20°。动点P,Q分别在直线BC上运动,且始终保持∠PAQ=100°。设BP=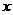 ,CQ=y,则y与
,CQ=y,则y与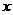 之间的函数关系用图象大致可以表示为( )
之间的函数关系用图象大致可以表示为( )

12.如图,正方形ABCD的面积为1,M是AB的中点,则图中阴影部分的面积是( )
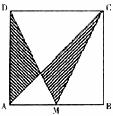
A. B.
B. C.
C. D.
D.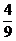
二、填空题:(每小题3分,共15分)
13.已知关于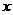 的方程:
的方程: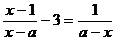 的解是
的解是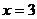 ,侧a的值为
.
,侧a的值为
.
14.现有50张大小、质地及背面图案均相同的北京奥运会吉祥物福娃卡片,正面朝下放置在桌面上,从中随机抽取一张并记下卡片正面所绘福娃的名字后原样放回,洗匀后再抽,不断重复上述过程,最后记录抽到欢欢的频率为20%,则这些卡片中欢欢约为 张.
15.线段AB,CD在平面直角坐标系中的位置如图所示,O为坐标原点。若线段AB上一点P的坐标为(a,b),则直线OP与线段CD的交点的坐标为 .
16.如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为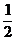 的半圆后得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3,P4,…Pn,…,记纸板Pn的面积为Sn,试计算求出S2=
;S3 ;并猜想得到
的半圆后得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3,P4,…Pn,…,记纸板Pn的面积为Sn,试计算求出S2=
;S3 ;并猜想得到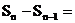 (n≥2).
(n≥2).

17.某市处理污水,需要铺设一条长为1000m的管道,为了尽量减少施工对交通所造成的影响,实际施工时,每天比原计划多铺设10米,结果提前5天完成任务。设原计划每天铺设管道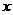 m,则可得方程
.
m,则可得方程
.
三.解答题:(共7小题,共69分)
18.(每小题5分,共10分)
(1)计算: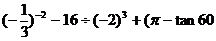 °
°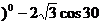 °
°
(2)解不等式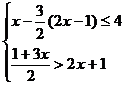 把解集表示在数轴上,并求出不等式组的整数解。
把解集表示在数轴上,并求出不等式组的整数解。
19.(本题满分1分)
为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图。
如下所示:
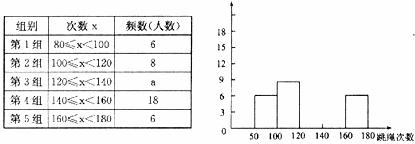
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)若八年级学生一分钟跳绳次数(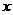 )达标要求是:
)达标要求是: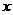 <120不合格;120≤
<120不合格;120≤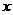 <140,为合格;140≤
<140,为合格;140≤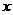 <160为良;
<160为良;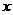 ≥160为优。根据以上信息,请你给学校或八年级同学提一条合理化建议:
.
≥160为优。根据以上信息,请你给学校或八年级同学提一条合理化建议:
.
20.(本题满分7分)
如图,已知:梯形ABCD中,AD//BC,E为AC的中点,连接DE并延长交BC于点F,连接AF.
(1)求证:AD=CF;
(2)在原有条件不变的情况下,请你再添加一个条件(不再增添辅助线),使四边形AFCD成为菱形,并说明理由。

21.(本小题满分8分)
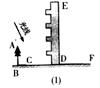
高为12米的教学楼ED前有一棵大树AB,如图(1).
(1)某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.5米,DF=7.5米,求大树AB的高度;
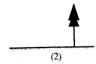
(2)现有皮尺和高为h米的测角仪,请你设计另一种测量大树AB高度的方案,要求:
①在图(2)中,画出你设计的测量方案示意图,并将应测量的数据标记在图上(长度用字母m,n……表示,角度用希腊字母 ,
, ……表示);
……表示);
②根据你所画出的示意图和标注的数据,求出大树的高度(用字母表示).
22.(本题满分11分)
工业园区某消毒液工厂,今年四月份以前,产量与销售量均为500箱。进入四月份后,每天的产量保持不变,市场需求量不断增加。如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象。
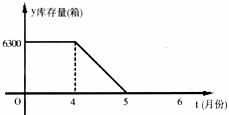
(1)四月份的平均日销售量为多少箱?
(2)该厂什么时候开始出现供不应求的现象,此时日销售量为多少箱?
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于四月份的平均日销售量。现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:

请问:有哪几种购买设备的方案?若为了使日产量最大,应选择哪种方案?
23.(本题满分11分)
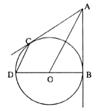
如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B8、C,⊙O的直径BD为6,连结CD、AO.
(1)求证:CD//AO;
(2)设CD=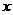 ,AO=y,求y与
,AO=y,求y与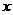 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量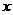 的取值范围;
的取值范围;
(3)若AO+CD=11,求AB的长.
24.(本题满分12分)
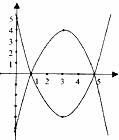
如图,已知与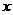 轴交于点A(1,0)和B(5,0)的抛物线
轴交于点A(1,0)和B(5,0)的抛物线 的顶点为C(3,4),抛物线
的顶点为C(3,4),抛物线 与
与 关于
关于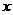 轴对称,顶点为
轴对称,顶点为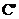 .
.
(1)求抛物线 的函数关系式;
的函数关系式;
(2)已知原点O,定点D(0,4), 上的点P与
上的点P与 上的点P’始终关于
上的点P’始终关于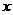 轴对称,则当点P运动到何必时,以点D,O,P,P’为顶点的四边形是平行四边形?
轴对称,则当点P运动到何必时,以点D,O,P,P’为顶点的四边形是平行四边形?
(3)在 上是否存在点M,使△ABM是以AB为斜边且一个角为30°的直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
上是否存在点M,使△ABM是以AB为斜边且一个角为30°的直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com