
2007-2008学年度淄博市张店第二学期初三学业水平自我诊断
数学试卷
一、精心选一选,相信自己的判断!
1.下列条件不能判定两个三角形全等的公理是( )
A.SAS B.ASA C.AAS D.SSA
2.用配方法解方程 ,经过配方得到( )
,经过配方得到( )
A. B.
B.
C. D.
D.
3.下列命题中,逆命题不正确的是( )
A.两直线平行,同旁内角互补 B.全等三角形的对应角相等
C.直角三角形两锐角互余 D.面积相等的两个三角形全等
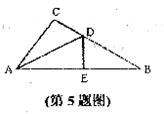
4.如图,△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数为( )

A.15° B.30° C.50° D.65°
5.在△ABC中,三边长分别为a、b、c,且满足 ,则这个三角形是( )
,则这个三角形是( )
A.等边三角形 B.等腰三角形 C.等腰直角三角形 D.以上都不对
6.下列方程是关于 的一元二次方程的是( )
的一元二次方程的是( )
A. B.
B.
C. D.
D.
7.已知∠AOB=30°,点P在∠AOB内部,p1与p关于OB对称,p2与p关于OA对称,则p1、O、p2三点构成的三角形是( )
A.直角三角形 B.钝角三角形 C.等腰三角形 D.等边三角形
二、认真填一填,试试自己的身手!
1.关于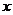 的方程
的方程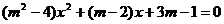 ,当m 时,方程是一元二次方程,当m
时,方程是一元一次方程.
,当m 时,方程是一元二次方程,当m
时,方程是一元一次方程.
2.关于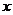 的一元二次方程
的一元二次方程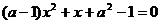 的一个根是0,
的一个根是0,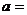 ,则另一个根是
.
,则另一个根是
.
3.若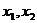 是方程
是方程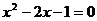 的两根,则
的两根,则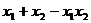 =
.
=
.
4.利用反证法证明“一个三角形中至多有一个直角”时,应首先提出的假设是
.
5.如图,有一张直角三角形的纸片,两直角边AC=
6.已知等腰三角形的底边长为
7.如图,△ABC中,AB=
三、做一做,尽显自己的能力!
1.选择合适方法,解下列一元二次方程
(1)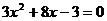
(2)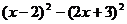
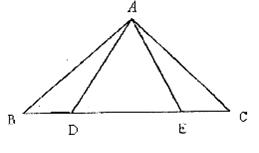
2.已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE.
求证:BD=CE
3.已知关于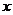 的方程
的方程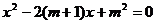 .
.
(1)若方程有两个相等的实数根,求m的值;
(2)当m选取一个合适的整数,使方程有两个不相等的实数根,并求出这两个根.
4.已知等腰三角形底边长为8,腰长是方程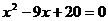 的一个根,求这个三角形的面积.
的一个根,求这个三角形的面积.
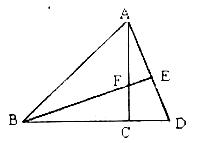
5.如图,在△ABD中,AC⊥BD,垂足为点C,BE与AC相交于点F,AC=BC,CD=CF,
求证:(1)∠DBF=∠CAD;
(2)BE⊥AD.
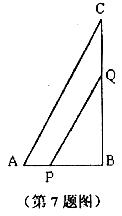
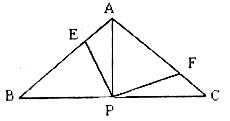
6.已知:如图,△ABC中,AB=AC,∠BAC=90°,P是BC中点,∠EPF=90°.
求证:AE=CF
7.西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元?
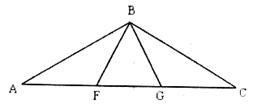
8.已知:如图,△ABC中,BA=BC,∠ABC=108°,F、G在边BC上,且AF=BF,BG=CG.
求证:点F、G是线段AC的黄金分割点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com