
2008-2009学年度聊城市高唐县第一学期九年级期末学业水平评价
数学试卷
(时间90分钟,满分120分)
第Ⅰ卷(选择题 共48分)
一、选择题(本题共12个小题,每小题4分。共48分.在每小题给出的四个选项中,只有一项符合题目要求)
1.在下列二次根式中与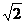 是同类二次根式的是( )
是同类二次根式的是( )
A.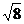 B.
B.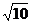 C.
C.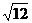 D.
D.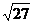
2.关于x的一元二次方程x2―3x=a2的一个根是4,则a的值为( )
A.2
B.?
3.已知直角三角形ABC中,斜边AB的长为m,∠B=50°。,则直角边BC的长是( )
A.msin50° B.mcos50° C.mtan50° D.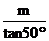
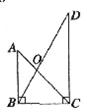
4.将一副三角板按图所示叠放,则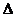 AOB与
AOB与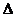 DOC的面积之比等于( )
DOC的面积之比等于( )
A.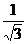 B.
B.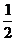 C.
C.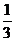 D.
D.
5.如图,将半径为
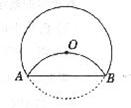
A.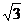 cm
C.
cm
C.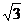 cm D.2
cm D.2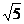 cm
cm
6.已知:如图,点E(?4,2),点F(?1,?l),以O为位似中心,按比例尺l:2,把△EFO缩小,则点E的对应点E’的坐标为( )
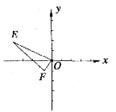
A.(2,?l)或(?2,1) B.(8,?4)或(?8,1)
C.(2,?l) D.(8,?4)
7.如图,在平地上种植树时,要求株距(相邻两树间的水平距离)为4m。如果在坡度为0.5的山坡上种植树,也要求株距为4m,那么相邻两树间的坡面距离约为( )
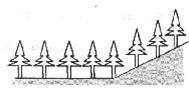
A.4.5m B.4.6rn C.6 m D.8m
8.在李咏主持的“幸运52”栏目中,曾有一种竞猜游戏,游戏规则是:在20个商标牌中,有五个商标牌的背面注明了一定的奖金,其余商标牌的背面是一张“哭脸”,若翻到“哭脸”就不获奖,参与这项游戏的观众有三次翻牌的机会,且翻过的牌不能再翻。有一位观众已翻拍两次,一次获奖一次不获奖,那么这位观众第三次翻牌获奖的概率是( )
A. B.
B.
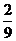 C.
C.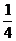 D.
D.
9.用一块铁皮制作一个圆锥模型,要求圆锥的母线长为l2cm,底面圆的半径为5cm,那么,这个圆锥模型的侧面展开扇形铁皮的圆心角度数为( )
A.90° B.120° C.150° D.240°
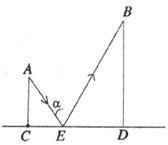
10.如图,CD是平面镜,光线从A点射入,经CD上点E反射后照射到B点,若入射角为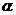 (若入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan
(若入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan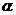 的值为(
)
的值为(
)
A.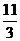 B.
B.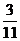 C.
C.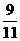 D.
D.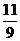
11.据2008年5月8日《台州晚报》报导,今年五一黄金周台州市旅游景点共接待游客334万人,旅游总收入约9亿元。已知该市2006年五一黄金周旅游总收入为6.25亿元,那么这两年同期旅游总收入的年平均增长率为( )
A.12% B.16% C.20% D.25%
12.与抛物线y=x2-2x-4关于y轴对称的图象表示的函数关系式是( )
A.y=-x2+2x+4. B.y=x2+2x+4
C.y=x2+2x-4 D.y=x2-2x+4
第Ⅱ卷(非选择题共72分)
二、填空题(本题共5个小题,每小题4分,共20分。将最后结果直接填在答题卷的相应位置)
13.写出一个开口向上,顶点是坐标原点的二次函数的表达式:_______________。
14.关于x的方程3x(x+2)=5(x+2)的解为______________________。
15.如图,∠ACB=∠ADC=900,AC=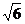 ,AD=2,则当AB=_____________时,这两个直角三角形相似。
,AD=2,则当AB=_____________时,这两个直角三角形相似。

16.如图,点O在Rt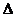 ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连接OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么,
ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连接OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么, 的值约为___________(π取3.14)
的值约为___________(π取3.14)
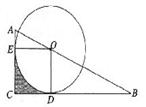
17.如图,一个以150的倾斜角斜靠在墙面上的梯子,将其扶起到使其倾斜角为750,如果梯子的总长为l.80米,则AC______________米(结果保留三个有效数字,参考数据:sinl50≈0.26,cosl50≈0.97,tanl50≈0.27)。

三、解答题(本题共6个小题,共52分.解答应写出必要的文字说明、证明过程或推演步骤)
18.(本题满分6分)
用配方法解方程2x2―5x+1=0.
19.(本题满分8分)
为举办2008年奥运会,须改变某市的交通状况。在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为600,树的底部B点的俯角为300.
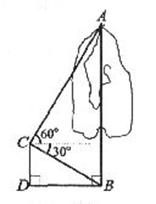
问:距离B点8米远的保护物是否在危险区内?
20.(本题满分8分)
如图,将边长为2的正方形ABCD折叠,使顶点A落在CD边上,即点M,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.
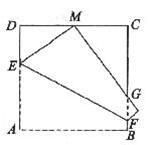
(1)求证: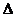 DEM~△CMG
DEM~△CMG
(2)当点M位于CD的中点时,求 DEM三边的长。
DEM三边的长。
21.(本题满分8分)
如图,P是⊙O的半径OA上的一点,D在⊙O上,且PD=PO.过点D作⊙O的切线交OA的延长线于点C,延长DP交⊙O于K,连接KO,OD.
(1)求证:PC=PD;
(2)若该圆半径为5,CD∥KO,请求出OC的长.
22.(本题满分l0分)
小军与小玲共同发明了一种“字母棋”,进行比胜负的游戏。他们用四种字母做成十枚棋子,其中A棋一枚,B棋两枚,C棋三枚,D棋四枚。“字母棋”的游戏规则为:
①游戏时两人各摸一枚进行比赛称一轮比赛,先摸者摸出的棋不放回;
②A棋胜B棋、C棋;B棋胜C棋、D棋;C棋胜D棋;
③相同棋子不分胜负。
(1)若小玲先摸,问小玲摸到C棋的概率是多少?
(2)已知小玲先摸到了C棋,小军在剩余的9枚棋中随即摸一枚,问这一轮中小玲胜小军的概率是多少?
(3)已知小玲先摸一枚棋,小军在剩余的9枚棋中随即摸一枚,问这一轮中小玲摸到哪种棋胜小军的概率最大?
23.(本题满分l2分)
如图 中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A和B。
中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A和B。
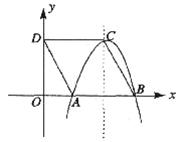
(1)求点A、B、C的坐标;
(2)若抛物线向上平移后恰好经过点D,求平移后抛物线的解析式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com