
2009年曲阜师大附中第二次中考模拟考试
数学试卷
第Ⅰ卷(选择题)
一、选择题(下列各题的四个选项中,只有一项符合题意。)
1.化简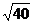 的结果是
的结果是
A.10 B. C.
C. D.20
D.20
2.在下列图形中,既是轴对称图形,又是中心对称图形的是

3.
A. 元 B.
元 B.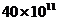 元 C.
元 C. 元 D.
元 D.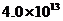 元
元
4.小华所在学习小组的同学们,在向雷锋叔叔学习月活动中,主动到附近的几个社区帮助爷爷、奶奶们作些力所能及的劳动。他们记录的各个社区参加其中一次活动的人数如下:33,32,32,31,28,26,32,那么这组数据的众数和中位数分别是
A.32,31 B.32,
5.如下图是某几何体的三视图及相关数据,则下面判断正确的是
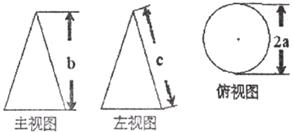
A.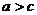 B.
B.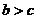 C.
C.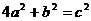 D.
D.
6.下图中的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各自发表了下述见解:
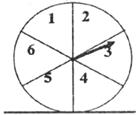
甲:如果指针前三次都停在3号扇形,下次就一定不会停在3号扇形了。
乙:只要指针连续转六次,一定会有一次停在6号扇形。
丙:指针停在奇数号扇形的概率和停在偶数号扇形的概率相等。
丁:第一次指针停在6号扇形,则下一次指针停在6号扇形的概率为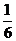 。
。
其中你认为正确的见解有( ).
A.1个 B.2个 C.3个 D.4个
7.如下图,P为平行四边形ABCD的对称中心,以P为圆心作圆,过点P的任意直线与圆P相交于点M、N,则线段BM、DN的大小关系是

A.BM<DN B.BM>DN C.BM=DN D.无法确定
8.在一个可以改变容积的密闭容器内,装有一定质量 的某种气体,当改变容积V时,气体的密度
的某种气体,当改变容积V时,气体的密度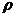 也随之改变。
也随之改变。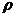 与V在一定范围内满足
与V在一定范围内满足 ,它的图像如下图所示,则该气体的质量
,它的图像如下图所示,则该气体的质量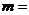

A.
9.如下图,是由10把相同的折扇组成的“蝶恋花”(左图)和梅花图案(右图)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为

A.36° B.42° C.45° D.48°
10.下列计算正确的是
A.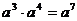 B.
B.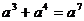 C.
C.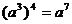 D.
D.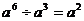
11.如下图, 分别表示苹果、梨、桃子的质量,同类水果质量相等,则下列关系正确的是
分别表示苹果、梨、桃子的质量,同类水果质量相等,则下列关系正确的是

A. B.
B. C.
C.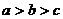 D.
D.
12.如下图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为
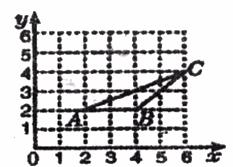
A.(2,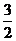 ) B.(2,
) B.(2,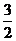 )或(-2,
)或(-2,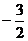 )
)
C.(-2,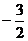 ) D.(8,6)或(-8,-6)
) D.(8,6)或(-8,-6)
第Ⅱ卷(非选择题)
二、填空题(只要求填写最后结果)
13.方程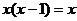 的解是__________。
的解是__________。
14.如下图,直线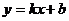 分别交
分别交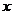 轴和
轴和 轴于点A、B,则关于
轴于点A、B,则关于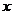 的不等式
的不等式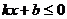 的解为__________。
的解为__________。

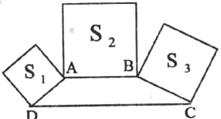
15.如下图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的关系是__________。
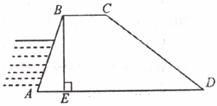
16.如下图所示,邹城市西苇水库坝堤的横断面是梯形ABCD,BC∥AD,迎水坡长 ,则坝堤的高BE为__________米。
,则坝堤的高BE为__________米。
17.已知,如下图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°。给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④AE=BC。其中正确结论的序号是__________。(填写序号)

18.定义: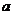 是不为1的有理数,我们把
是不为1的有理数,我们把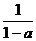 称为
称为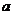 的差倒数。如:2的差倒数是
的差倒数。如:2的差倒数是 ,-1的差倒数是
,-1的差倒数是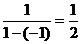 。已知
。已知 ,
, 是
是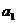 的差倒数,
的差倒数,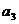 是
是 的差倒数,
的差倒数, 是
是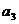 的差倒数,……,依此类推,则
的差倒数,……,依此类推,则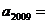 __________。
__________。
三、解答题(解答应写出文宇说明、证明过程或推演步骤)
19.先化简式子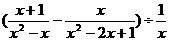 ,然后请选取一个你最喜欢的
,然后请选取一个你最喜欢的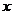 值代入求出这个式子的值。
值代入求出这个式子的值。
20.某市在中心城区范围内,选取重点示范路口进行交通文明状况满意度调查,将调查结果的满意度分为:不满意、一般、较满意、满意和非常满意,依次以红、橙、黄、蓝、绿五色标识。今年五月发布的调查结果中,橙色与黄色标识路口数之和占被调查路口总数的15%。结合未画完整的图中所示信息,回答下列问题:
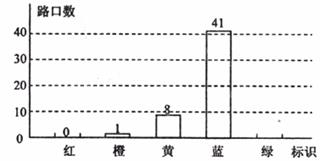
(1)此次被调查的路口总数是____________;
(2)将图中绿色标识部分补画完整,并标上相应的路口数;
(3)此次被调查路口的满意度能否作为该市所有路口交通文明状况满意度的一个随机样本?
21.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中。用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现。小明在研究垂直于直径的弦的性质过程中(如下图,直径AB⊥弦CD于E),设AE=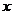 ,BE=
,BE= ,他用含
,他用含 的式子表示图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数
的式子表示图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数 的不等式,你也能发现这个不等式吗?
的不等式,你也能发现这个不等式吗?
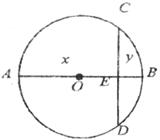
(1)请你写出他用含 的式子表示图中的弦CD的长度推导过程。
的式子表示图中的弦CD的长度推导过程。
(2)写出你发现的不等式____________。
22.如下图,在△ABC中,AB=AC,点E、F分别在AC、AB上,EF∥BC,将△AEF向上翻折,得到△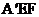 ,再展开。
,再展开。
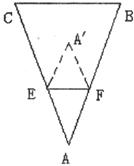
(1)求证:四边形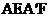 是菱形。
是菱形。
(2)直接写出当等腰△ABC满足什么条件时,四边形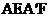 将变成正方形?
将变成正方形?
(3)当点A恰好落在BC上时,直接写出EF与BC的数量关系。
23.已知小明骑车和步行的速度分别为
24.如下图,桌面内,直线 上摆放着两块大小相同的直角三角板,它们中较小直角边的长为
上摆放着两块大小相同的直角三角板,它们中较小直角边的长为
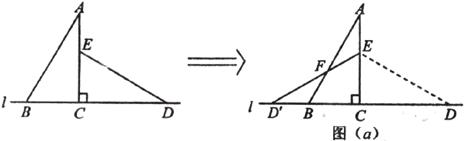
(1)将△ECD沿直线AC翻折到图(a)的位置。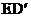 与AB相交于点F,请证明:
与AB相交于点F,请证明: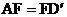 ;
;
(2)将△ECD沿直线 向左平移到下图(b)的位置,使E点落在AB上,你可以求出平移的距离,试试看;
向左平移到下图(b)的位置,使E点落在AB上,你可以求出平移的距离,试试看;
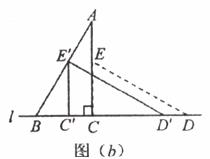
(3)将△ECD绕点C逆时针方向旋转到上图(c)的位置,使E点落在AB上。请求出旋转角的度数。

25.某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
A
B
成本(万元ㄍ套)
25
28
售价(万元ㄍ套)
30
34
(1)该公司对这两种户型住房有哪几种建房方案?
(2)该公司如何建房获得利润最大?
(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高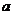 万元(
万元(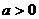 ),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?(注:利润=售价-成本)
),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?(注:利润=售价-成本)
26.已知:在Rt△ABO中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为轴,建立如下图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处。

(1)求点C的坐标;
(2)若抛物线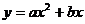
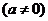 经过C、A两点,求此抛物线的解析式;
经过C、A两点,求此抛物线的解析式;
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作 轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com