
2009年湖南省怀化市初中毕业学业考试
数学试卷
一、选择题(每小题3分,共30分)
1.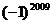 的相反数是(
)
的相反数是(
)
A.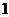 B.
B.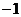 C.
C. D.
D.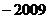
2.下列运算正确的是( )
A. B.
B.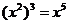 C.
C.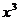 ?
?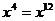 D.
D. 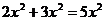
3.不等式组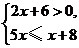 的解集在下列数轴上表示正确的是( )
的解集在下列数轴上表示正确的是( )

4.如图, 、
、 分别是
分别是 、
、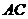 的中点,则
的中点,则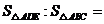 ( )
( )
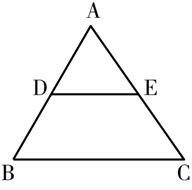
A.1∶2 B.1∶3
C.1∶4 D.2∶3
5.下列事件中,属于必然事件的是( )
A.某种彩票的中奖率为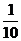 ,佳佳买
,佳佳买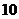 张彩票一定能中奖
张彩票一定能中奖
B.“小沈阳”明年一定能上春节联欢晚会表演节目
C.抛一枚硬币,正面朝上的概率为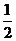
D.这次数学考试乐乐肯定能考满分
6.如图,这是一个正三棱柱,则它的俯视图为( )

7.分式方程 的解是( )
的解是( )
A.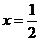 B.
B.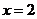 C.
C.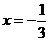 D.
D. 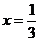
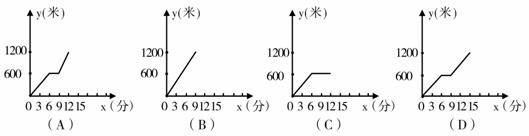
8.小敏家距学校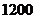 米,某天小敏从家里出发骑自行车上学,开始她以每分钟
米,某天小敏从家里出发骑自行车上学,开始她以每分钟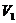 米的速度匀速行驶了
米的速度匀速行驶了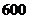 米,遇到交通堵塞,耽搁了
米,遇到交通堵塞,耽搁了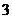 分钟,然后以每分钟
分钟,然后以每分钟 米的速度匀速前进一直到学校
米的速度匀速前进一直到学校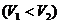 ,你认为小敏离家的距离
,你认为小敏离家的距离 与时间
与时间 之间的函数图象大致是( )
之间的函数图象大致是( )
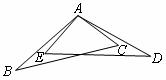
9.如图,在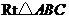 中,
中,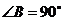 ,
,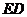 是
是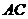 的垂直平分线,交
的垂直平分线,交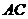 于点
于点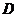 ,交
,交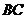 于点
于点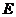 .已知
.已知 ,则
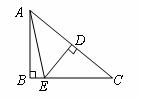
,则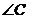 的度数为( )
的度数为( )
A.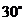 B.
B.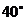
C.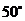 D.
D.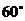
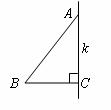
10.如图,在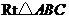 中,
中,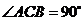 ,
,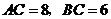 ,将
,将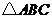 绕
绕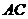 所在的直线
所在的直线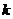 旋转一周得到一个旋转体,则该旋转体的侧面积为( )
旋转一周得到一个旋转体,则该旋转体的侧面积为( )
A.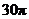 B.
B.
C.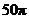 D.
D.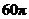
二、填空题(每小题3分,共30分)
11.若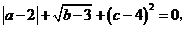 则
则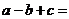 .
.
12.因式分解: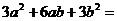 .
.
13.方程组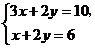 的解为 .
的解为 .
14.已知反比例函数 经过点
经过点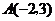 ,则其函数表达式为
.
,则其函数表达式为
.
15.如图,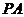 、
、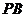 分别切⊙
分别切⊙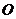 于点
于点 、
、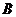 ,点
,点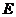 是⊙
是⊙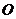 上一点,且
上一点,且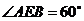 ,则
,则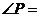 __ ___度.
__ ___度.

16.如图,已知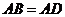 ,
,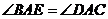 ,要使
,要使 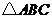 ≌
≌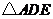 ,可补充的条件是
(写出一个即可).
,可补充的条件是
(写出一个即可).
17.亲爱的同学们,我们在教材中已经学习了:①等边三角形;②等腰梯形;③平行四边形;④等腰三角形;⑤圆.在以上五种几何图形中,既是轴对称图形,又是中心对称图形的是 .
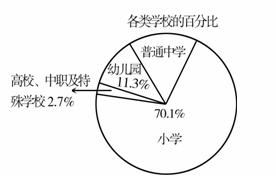
18.怀化市现有各类学校 所,图是各类学校所占比例的扇形统计图,由图可知普通中学有 所(用四舍五入法精确到个位).
所,图是各类学校所占比例的扇形统计图,由图可知普通中学有 所(用四舍五入法精确到个位).
19.从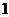 ,
,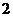 ,
,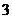 ,
,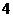 这四个数字中任意取出两个不同的数字,取出的两个数字都是偶数的概率是 .
这四个数字中任意取出两个不同的数字,取出的两个数字都是偶数的概率是 .
20.如图,小明从 地沿北偏东
地沿北偏东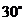 方向走
方向走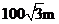 到
到 地,再从
地,再从 地向正南方向走
地向正南方向走
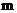 到
到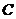 地,此时小明离
地,此时小明离 地
地 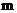 .
.

三.解答题(本大题6个小题,满分40分)
21.(本题满分6分)
先化简,再求值: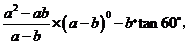 其中
其中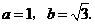
22.(本题满分6分)
如图,P是∠BAC内的一点,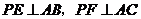 ,垂足分别为点
,垂足分别为点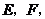
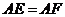 .
.
求证:
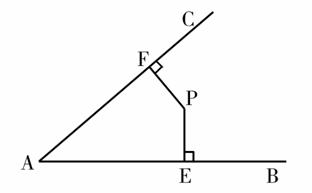
(1)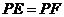 ;
;
(2)点P在∠BAC的角平分线上.
23.(本题满分6分)
怀化市管辖13个县(市、区),2008年怀化市国民经济生产总值达到了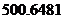 亿元. 下表是2008年怀化市年各县(市、区)国民经济生产总值的统计表(单位:亿元).
亿元. 下表是2008年怀化市年各县(市、区)国民经济生产总值的统计表(单位:亿元).
县(市、区)
国民经济生产总值
鹤城区
101.3773
洪江区
17.0612
中方县
32.4279
沅陵县
70.5137
辰溪县
37.4963
溆浦县
55.9430
会同县
26.0289
麻阳县
23.4570
新晃县
19.1498
芷江县
35.7028
靖州县
27.7013
通道县
13.5767
洪江市
40.2122
(1)计算怀化市2008年各县(市、区)国民经济生产总值的平均值(用四舍五入法精确到0.0001);
(2)求出各县(市、区)国民经济生产总值这组数据的中位数;
(3)上述平均值、中位数哪一个数更能说明怀化市各县(市、区)国民经济生产总值的水平?
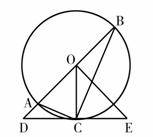
24.(本题满分6分)
如图,直线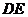 经过⊙
经过⊙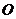 上的点
上的点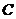 ,并且
,并且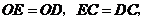 ⊙
⊙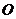 交直线
交直线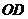 于
于 、
、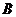 两点,连接
两点,连接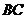 ,
,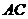 ,
,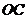 .求证:
.求证:
(1)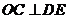 ;
;
(2)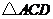 ∽
∽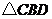 .
.
25.(本题满分6分)
如图,已知二次函数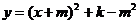 的图象与
的图象与 轴相交于两个不同的点
轴相交于两个不同的点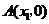 、
、 ,与
,与 轴的交点为
轴的交点为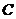 .设
.设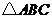 的外接圆的圆心为点
的外接圆的圆心为点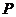 .
.
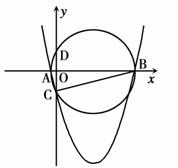
(1)求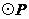 与
与 轴的另一个交点D的坐标;
轴的另一个交点D的坐标;
(2)如果 恰好为
恰好为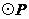 的直径,且
的直径,且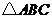 的面积等于
的面积等于 ,求
,求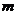 和
和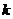 的值.
的值.
26.(本题满分10分)
如图,在直角梯形OABC中, OA∥CB,A、B两点的坐标分别为A(15,0),B(10,12),动点P、Q分别从O、B两点出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q也同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,射线QE交 轴于点F.设动点P、Q运动时间为t(单位:秒).
轴于点F.设动点P、Q运动时间为t(单位:秒).
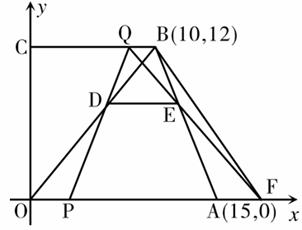
(1)当t为何值时,四边形PABQ是等腰梯形,请写出推理过程;
(2)当t=2秒时,求梯形OFBC的面积;
(3)当t为何值时,△PQF是等腰三角形?请写出推理过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com