
2009年广东省湛江市初中毕业生学业考试
数学试卷
说明:
1.本试卷满分150分,考试时间90分钟.
2.本试卷共6页,共5大题.
3.答题前,请认真阅读答题卡上的“注意事项”,然后按要求将答案写在答题卡相应的位置上.
4.请考生保持答题卡的整洁,考试结束,将试卷和答题卡一并交回.
注意:在答题卡上作图必须用黑色字迹的钢笔或签字笔.
一、选择题:本大题10个小题,其中1~5每小题3分,6~10每小题4分,共35分.在每小题给出的四个选项中,只有一项是符号题目要求的)
1.下列四个数中,在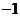 和
和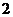 之间的数是(
)
之间的数是(
)
A.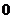 B.
B.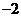 C.
C.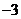 D.
D.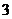
2.下列各式中,与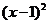 相等的是( )
相等的是( )
A.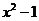 B.
B.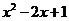 C.
C.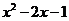 D.
D.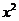
3.湛江是个美丽的海滨城市,三面环海,海岸线长达
A.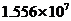 B.
B. C.
C.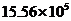 D.
D.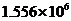
4.在下图的几何体中,它的左视图是( )
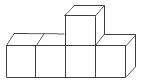
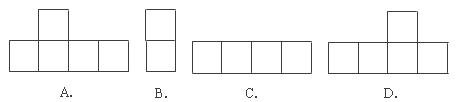
5.沃尔玛商场为了了解本商场的服务质量,随机调查了本商场的100名顾客,调查的结果如图所示,根据图中给出的信息,这100名顾客中对该商场的服务质量表示不满意的有( )
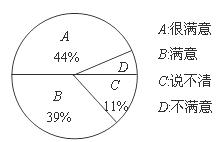
A.6人 B.11人 C.39人 D.44人
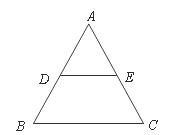
6.如图,在等边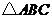 中,
中,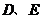 分别是
分别是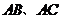 的中点,
的中点,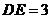 ,则
,则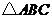 的周长是( )
的周长是( )
A.6 B.
7.如图,在平面直角坐标系中,菱形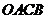 的顶点
的顶点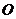 在原点,点
在原点,点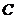 的坐标为
的坐标为 ,点
,点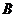 的纵坐标是
的纵坐标是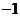 ,则顶点
,则顶点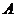 的坐标是( )
的坐标是( )
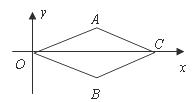
A.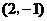 B.
B.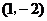 C.
C.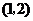 D.
D.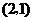
8.根据下图所示程序计算函数值,若输入的 的值为
的值为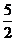 ,则输出的函数值为(
)
,则输出的函数值为(
)
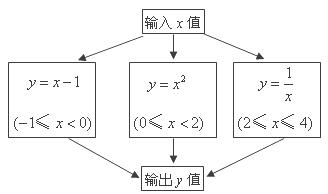
A.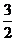 B.
B.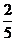 C.
C.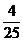 D.
D.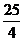
9.下列说法中:
①4的算术平方根是±2;
②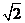 与
与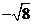 是同类二次根式;
是同类二次根式;
③点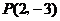 关于原点对称的点的坐标是
关于原点对称的点的坐标是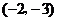 ;
;
④抛物线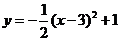 的顶点坐标是
的顶点坐标是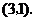
其中正确的是( )
A.①②④ B.①③ C.②④ D.②③④
10.如图,小林从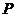 点向西直走
点向西直走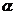 ,再走
,再走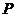 ,则
,则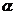 ( )
( )
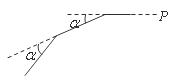
A.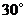 B.
B.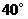 C.
C.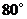 D.不存在
D.不存在
二、填空题:本大题共10个小题,其中11~15每小题3分,16~20每小题4分,共35分.
11.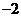 的相反数是
.
的相反数是
.
12.要使分式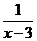 有意义,则
有意义,则 的取值范围是
.
的取值范围是
.
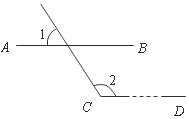
13.如图,已知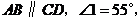 则
则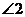 =
.
=
.
14.分解因式: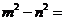 .
.
15.已知在一个样本中,40个数据分别落在4个组内,第一、二、四组数据个数分别为5、12、8,则第三组的频数为 .
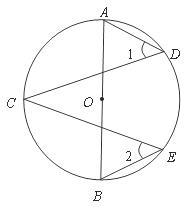
16.如图,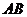 是
是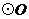 的直径,
的直径,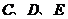 是
是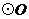 上的点,则
上的点,则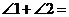
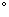 .
.
17.一件衬衣标价是132元,若以9折降价出售,仍可获利10%,则这件衬衣的进价是
元.
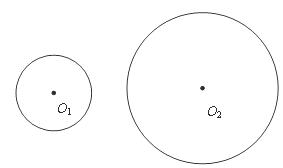
18.如图,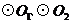 的直径分别为
的直径分别为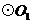 向
向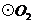 平移,当
平移,当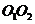 = cm时,
= cm时,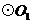 与
与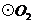 相切.
相切.
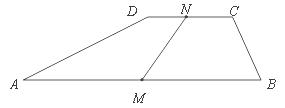
20.如图,在梯形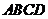 中,
中,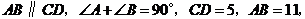 点
点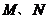 分别为
分别为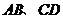 的中点,则线段
的中点,则线段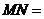 .
.
三、解答题:本大题共2小题,每小题8分,共16分.
21.如图,一只蚂蚁从点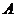 沿数轴向右直爬2个单位到达点
沿数轴向右直爬2个单位到达点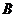 ,点
,点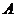 表示
表示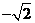 ,设点
,设点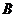 所表示的数为
所表示的数为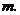
(1)求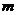 的值;
的值;
(2)求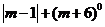 的值.
的值.

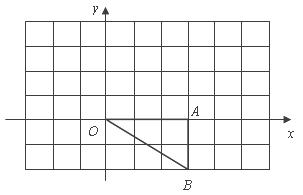
22.如图,点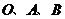 的坐标分别为
的坐标分别为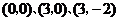 ,将
,将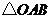 绕点
绕点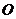 按逆时针方向旋转
按逆时针方向旋转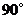 得到
得到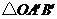 .
.
(1)画出旋转后的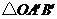 ,并求点
,并求点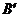 的坐标;
的坐标;
(2)求在旋转过程中,点 所经过的路径
所经过的路径 的长度.(结果保留
的长度.(结果保留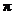 )
)
四、解答题:本大题共4小题,每小题10分,共40分.
23.某语文老师为了了解中考普通话考试的成绩情况,从所任教的九年级(1)、(2)两班各随机抽取了10名学生的得分,如图所示:
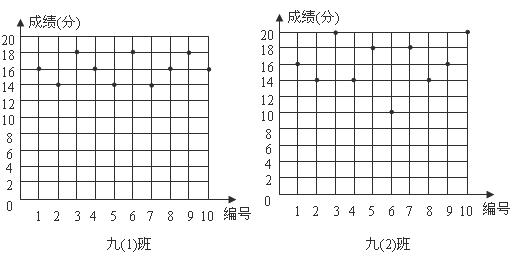
(1)利用图中的信息,补全下表:
班级
平均数(分)
中位数(分)
众数(分)
九(1)班
16
16
九(2)班
16
(2)若把16分以上(含16分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀.
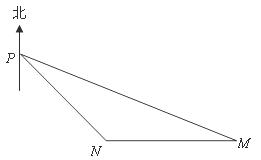
24.如图,某军港有一雷达站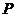 ,军舰
,军舰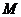 停泊在雷达站
停泊在雷达站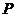 的南偏东
的南偏东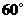 方向36海里处,另一艘军舰
方向36海里处,另一艘军舰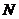 位于军舰
位于军舰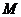 的正西方向,与雷达站
的正西方向,与雷达站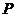 相距
相距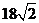 海里.求:
海里.求:
(1)军舰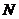 在雷达站
在雷达站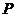 的什么方向?
的什么方向?
(2)两军舰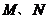 的距离.(结果保留根号)
的距离.(结果保留根号)
25.六张大小、质地均相同的卡片上分别标有1、2、3、4、5、6,现将标有数字的一面朝下扣在桌面上,从中随机抽取一张(放回洗匀),再随机抽取第二张.
(1)用列表法或树状图表示出前后两次抽得的卡片上所标数字的所有可能结果;
(2)记前后两次抽得的数字分别为m、n,若把m、n分别作为点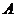 的横坐标和纵坐标,求点
的横坐标和纵坐标,求点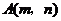 在函数
在函数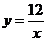 的图象上的概率.
的图象上的概率.
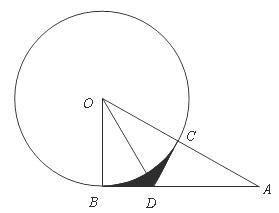
26.如图,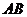 是
是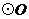 的切线,切点为
的切线,切点为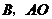 交
交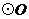 于点
于点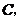 过点
过点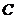 作
作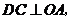 交
交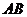 于点
于点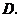
(1)求证: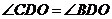 ;
;
(2)若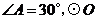 的半径为4,求阴影部分的面积.(结果保留
的半径为4,求阴影部分的面积.(结果保留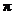 )
)
五、解答题:本大题共2小题,每小题12分,共24分.
27.某公司为了开发新产品,用A、B两种原料各360千克、290千克,试制甲、乙两种新型产品共50件,下表是试验每件新产品所需原料的相关数据:

A(单位:千克)
B(单位:千克)
甲
9
3
乙
4
10
(1)设生产甲种产品x件,根据题意列出不等式组,求出x的取值范围;
(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,写出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各生产多少件时,产品的成本总额最少?并求出最少的成本总额.
28.已知矩形纸片 的长为4,宽为3,以长
的长为4,宽为3,以长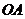 所在的直线为
所在的直线为 轴,
轴,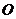 为坐标原点建立平面直角坐标系;点
为坐标原点建立平面直角坐标系;点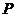 是
是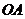 边上的动点(与点
边上的动点(与点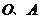 不重合),现将
不重合),现将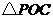 沿
沿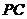 翻折得到
翻折得到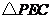 ,再在
,再在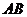 边上选取适当的点
边上选取适当的点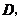 将
将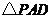 沿
沿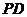 翻折,得到
翻折,得到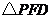 ,使得直线
,使得直线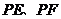 重合.
重合.
(1)若点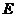 落在
落在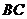 边上,如图①,求点
边上,如图①,求点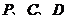 的坐标,并求过此三点的抛物线的函数关系式;
的坐标,并求过此三点的抛物线的函数关系式;
(2)若点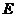 落在矩形纸片
落在矩形纸片 的内部,如图②,设
的内部,如图②,设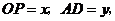 当
当 为何值时,
为何值时,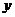 取得最大值?
取得最大值?
(3)在(1)的情况下,过点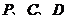 三点的抛物线上是否存在点
三点的抛物线上是否存在点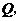 使
使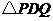 是以
是以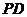 为直角边的直角三角形?若不存在,说明理由;若存在,求出点
为直角边的直角三角形?若不存在,说明理由;若存在,求出点 的坐标。
的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com