|
得分 评卷人
试题详情
将数列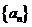 中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: 中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: 试题详情
试题详情
试题详情
试题详情
试题详情
(Ⅰ)设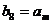 ,求 ,求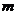 的值; 的值; 试题详情
试题详情
(Ⅲ)对于(Ⅱ)中的数列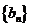 ,若上表中每一行的数按从左到右的顺序均构成公比为 ,若上表中每一行的数按从左到右的顺序均构成公比为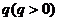 的等比数列,且 的等比数列,且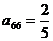 ,求上表中第 ,求上表中第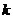 ( (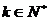 )行所有项的和 )行所有项的和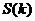 . . 闸北区09届高三数学(文)学科模拟考试 试题详情
一.填空题: 1. ; 2. ; 2. ;
3. ;
3. 4.2; 5.4; 4.2; 5.4; 6.45; 7. ; 8.8;
9.3; 10. ; 8.8;
9.3; 10. . . 二.选择题:11.B ; 12. C; 13. C. 三.解答题: 15.解:(Ⅰ)由已知可求得,正方形 的面积 的面积 ,……………………………2分 ,……………………………2分 所以,求棱锥 的体积 的体积 ………………………………………4分 ………………………………………4分 (Ⅱ)方法一(综合法) 设线段 的中点为 的中点为 ,连接 ,连接 , , 则 为异面直线OC与 为异面直线OC与 所成的角(或其补角) ………………………………..1分 所成的角(或其补角) ………………………………..1分 由已知,可得 , , 
 为直角三角形 ……………………………………………………………….2分 为直角三角形 ……………………………………………………………….2分
 , ……………………………………………………………….4分 , ……………………………………………………………….4分
 . .
所以,异面直线OC与MD所成角的大小 . …………………………..1分 . …………………………..1分 方法二(向量法) 以AB,AD,AO所在直线为 轴建立坐标系, 轴建立坐标系, 则 ,
……………………………………………………2分 ,
……………………………………………………2分  , , ,
………………………………………………………………………………..2分 ,
………………………………………………………………………………..2分
设异面直线OC与MD所成角为 , ,  .……………………………….. …………………………3分 .……………………………….. …………………………3分
 OC与MD所成角的大小为 OC与MD所成角的大小为 .…………………………………………………1分 .…………………………………………………1分 16.[解一]由已知,在 中, 中, , , ,………………………….2分 ,………………………….2分 由正弦定理,得  ……………………………6分 ……………………………6分 因此,  …………………………………………5分 …………………………………………5分  .……………………………………………………………………2分 .……………………………………………………………………2分
[解二] 延长 交地平线与 交地平线与 ,…………………………………………………………………3分 ,…………………………………………………………………3分 由已知,得 …………………………………………………4分 …………………………………………………4分 整理,得 ………………………………………………………………………8分 ………………………………………………………………………8分 17.[解](Ⅰ)函数 的定义域为 的定义域为 …………………………………………………………2分 …………………………………………………………2分  , ,
当 时,因为 时,因为 ,所以 ,所以 , ,  ,从而 ,从而 ,……………………………………………………..4分 ,……………………………………………………..4分
所以函数 的值域为 的值域为 .………………………………………………………………..1分 .………………………………………………………………..1分 (Ⅱ)假设函数 是奇函数,则,对于任意的 是奇函数,则,对于任意的 ,有 ,有 成立, 成立, 即  当 当 时,函数 时,函数 是奇函数.…………………………………………………………….3分 是奇函数.…………………………………………………………….3分
当 ,且 ,且 时,函数 时,函数 是非奇非偶函数.………………………………………….1分 是非奇非偶函数.………………………………………….1分  对于任意的 对于任意的 ,且 ,且 , ,
   ……………………………………………..4分 ……………………………………………..4分
 当 当 时,函数 时,函数 是递减函数.………………………………………………..1分 是递减函数.………………………………………………..1分
18.[解](Ⅰ)因为 ,且 ,且 边通过点 边通过点 ,所以 ,所以 所在直线的方程为 所在直线的方程为 .1分 .1分 设 两点坐标分别为 两点坐标分别为 . . 由 得
得 . . 所以 . ……………………………………………..4分 . ……………………………………………..4分 又因为 边上的高 边上的高 等于原点到直线 等于原点到直线 的距离. 的距离. 所以 , , . ……………………………………….3分 . ……………………………………….3分 (Ⅱ)设 所在直线的方程为 所在直线的方程为 , ……………………………………………..1分 , ……………………………………………..1分 由 得 得 . …………………………………..2分 . …………………………………..2分 因为 在椭圆上,所以 在椭圆上,所以 . ………………….. …………..1分 . ………………….. …………..1分 设 两点坐标分别为 两点坐标分别为 , , 则 , , , , 所以 .……………………………………………..3分 .……………………………………………..3分 又因为 的长等于点 的长等于点 到直线 到直线 的距离,即 的距离,即 .……………..2分 .……………..2分 所以 .…………………..2分 .…………………..2分 所以当 时, 时, 边最长,(这时 边最长,(这时 ) ) 此时 所在直线的方程为 所在直线的方程为 . ……………………………………………..1分 . ……………………………………………..1分 17.[解](Ⅰ)由题意, ……………………………6分 ……………………………6分 (Ⅱ)解法1:由 且 且 知 知  , , , ,
 , , , ,
因此,可猜测 ( ( ) ………………………………………………………4分 ) ………………………………………………………4分 将 , , 代入原式左端得 代入原式左端得 左端   即原式成立,故 为数列的通项.……………………………………………………….3分 为数列的通项.……………………………………………………….3分 用数学归纳法证明得3分 解法2:由  , , 令 得 得 ,且 ,且 即 ,……… ……………………………………………………………..4分 ,……… ……………………………………………………………..4分 所以 因此 , , ,..., ,..., 将各式相乘得 ………………………………………………………………………………3分 ………………………………………………………………………………3分 (Ⅲ)设上表中每行的公比都为 ,且 ,且 .因为 .因为 , , 所以表中第1行至第9行共含有数列 的前63项,故 的前63项,故 在表中第10行第三列,………2分 在表中第10行第三列,………2分 因此 .又 .又 ,所以 ,所以 .…………………………………..3分 .…………………………………..3分 则 . . …………………………………………2分 …………………………………………2分
| 