
寿光市2009年高考适应性训练试题
高三数学(文科)
2009.5
本试卷共4页,分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 复数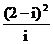 (i是虚数单位)在复平面上对应的点位于( )
(i是虚数单位)在复平面上对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知集合M={-1, 0, 1},N={x|x=ab, a, b∈M且a≠b},则集合M与集合N的关系是()

 A. M=N B.
M
A. M=N B.
M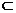 N C.
M
N C.
M 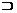 N D.
M
N D.
M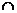 N=
N=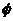
3. 在△ABC中,边a=2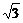 ,边c=
,边c=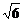 +
+ ,角B=45°,则边b的长为( )
,角B=45°,则边b的长为( )
 A.
A.
 B.
B.
 C.
C.
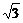 D.
2
D.
2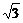
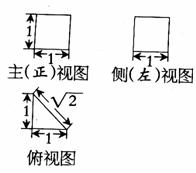
4. 已知某几何体的三视图如右图所示,它的表面积
是( )
A. 4+ B.
2+
B.
2+ C. 3+
C. 3+ D.
6
D.
6
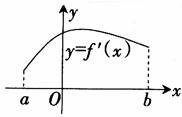 5. 已知f5′(x)是函数f (x)的函导数,在区间[a, b]上f ′(x)的图象如右图所示,如果f (a) f (b)<0,则函数f (x)在区间(a, b)上( )
5. 已知f5′(x)是函数f (x)的函导数,在区间[a, b]上f ′(x)的图象如右图所示,如果f (a) f (b)<0,则函数f (x)在区间(a, b)上( )
A. 至少有一个零点 B. 至多有一个零点
C. 没有零点 D. 必有唯一的零点
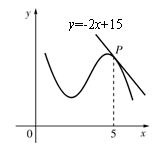 6.设α,β,γ是三个不重合的平面,m, n是两条不重合的直线,给出下列命题:①若α⊥β,β⊥γ,则α⊥γ;②若m∥α, n∥β, α⊥β,则m⊥n;③若α∥β,γ∥β,则α∥γ;④若α∥β且m与α,n与β所成的角相等,则m∥n。其中错误命题的个数为( )
6.设α,β,γ是三个不重合的平面,m, n是两条不重合的直线,给出下列命题:①若α⊥β,β⊥γ,则α⊥γ;②若m∥α, n∥β, α⊥β,则m⊥n;③若α∥β,γ∥β,则α∥γ;④若α∥β且m与α,n与β所成的角相等,则m∥n。其中错误命题的个数为( )
A. 0 B. 1 C. 2 D. 3
7.函数y=f(x)的图象在点P处的切线方程是y=-2x+15,如图,
则f(5)+ f ′(5)=( )
A.1 B. 2 C. 3 D. 4
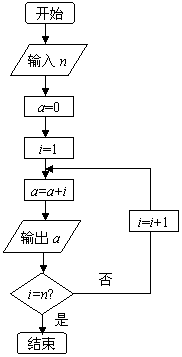 8. 若数列{an}的前n项由如图所示的程序框图中输出
8. 若数列{an}的前n项由如图所示的程序框图中输出
的a的值依次给出,则数列{an}的通项公式an=( )
A. 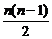 B.
n C.
n-1 D.
B.
n C.
n-1 D.

9. 抛物线y=ax2的焦点恰好为双曲线y2-x2=2的上焦点,则a=( )
A. 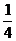 B.
B.
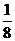 C.
C.
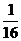 D.
1
D.
1
10. 设等差数列{an}中,a6+a10=16, a4=1,则a12的值是( )
A. 15 B. 30 C. 31 D. 64
11. 已知f (x)为偶函数,且f (2+x)=f (2-x),当-2≤x≤0时,f (x)=2x, an=f (n), n∈N*,则a2009=( )
A. 2009 B.
2 C.
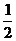 D.
-2
D.
-2
12. 函数f (x)=ax2-x-c的零点是-2,1,则函数y = f ( -x)的图象为( )
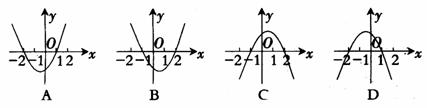
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷包括填空题和解答题共两个大题.
2.第Ⅱ卷所有题目的答案考生需用黑色签字笔答在“数学”答题卡指定的位置上.
 二、填空题:本大题共4小题,每小题4分,共16分.
二、填空题:本大题共4小题,每小题4分,共16分.
13. 如图,是在某一年全国少数民族运动会上,七位评委
为某民族舞蹈运动员打出的分数的茎叶统计图,去掉一个最高分
和一个最低分后,所剩数据的平均数为 ,方差为 .
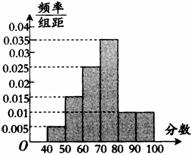 14. 统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如图所示,规定不低于60分为及格,不低于80分为优秀,则及格人数是 .
14. 统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如图所示,规定不低于60分为及格,不低于80分为优秀,则及格人数是 .
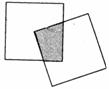 15. 现有一个关于平面图形的命题:如图,同一平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积为
15. 现有一个关于平面图形的命题:如图,同一平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积为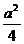 . 类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
. 类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
16. 定义一种运算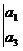
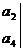 =a1a4-a2a3.
将函数f (x)=
=a1a4-a2a3.
将函数f (x)= 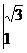
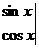 的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为 .
的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为 .
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知点A (2,0), B (0,2), C (cos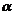 , sin
, sin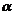 ).
).
(1)若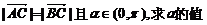 ;
;
(2)若f (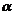 )=
)= 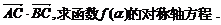
18.(本小题满分12分)
一个盒中放有除颜色不同外,其余完全相同的黑球和白球,其中黑球2个,白球3个;
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率;
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
19.(本小题满分12分)
数列{an}中,a1=-27,an+1+an=3n-54,(n∈N*).
(1)求证a1, a3, a5, …和a2, a4, a6,…分别成等差数列,并求数列{an}的通项公式;
(2)求数列{an}的前n(n为偶数)项和Sn的最小值.
20.(本小题满分12分)
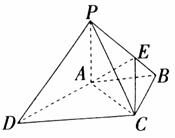 如图,四棱锥P―ABCD中,PA⊥底面ABCD,PC⊥AD。底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=1,点E在棱PB上,且PE=2EB.
如图,四棱锥P―ABCD中,PA⊥底面ABCD,PC⊥AD。底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=1,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求四棱锥P―ABCD的体积V;
(3)求证:PD∥平面EAC.
(注:棱锥体积=底面积×高÷3)
21.(本小题满分12分)
已知定点C(-1,0)及椭圆x2+3y2=5,过点C且斜率为k的直线与椭圆相交于不同的两点A,B.
(1)若线段AB中点的横坐标是-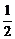 ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使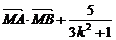 是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由。
是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由。
22.(本小题满分14分)
已知函数f (x)=
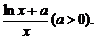
(1)求f(x)的极大值;
(2)若函数f (x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围
寿光市2009年高考适应性训练试题
一、选择题:
1. C 2. C 3. B 4.C 5. D 6. D 7. C 8. D 9. B 10. A 11. C 12. C
二、填空题:
13. 85,1.6 14. 800 15.  16.
16. 
三、解答题:
17.解: (1) ………………………1分
………………………1分

 ,
,
化简得 …………………………3分
…………………………3分

(2) )
)

令 Z),函数f(α)的对称轴方程为
Z),函数f(α)的对称轴方程为
 Z).………………………………………………………12分
Z).………………………………………………………12分
18. 解:(1)从盒中同时摸出两个球,有 种可能情况,…………2分
种可能情况,…………2分
摸出两球颜色恰好相同即两个黑球或两个白球,有1+ 种情况,……4分
种情况,……4分
故所求概率是 ………………………………………………………………6分
………………………………………………………………6分
(2)从盒中摸出一个球,放回后再摸出一个球,共有5×5=25种情况,……8分
若两球颜色不同,即“先黑后白”或“先白后黑”,共有2×3+3×2=12种可能情况,故所求概率是 ………………………………………………………………………12分
………………………………………………………………………12分
(本题也可一一列出基本事件空间后求解)
19.解:(1)an+1+an=3n-54, an+2+an+1=3(n+1)-54.
两式相减得an+2-an=3(n∈N*),
∴数列a1,a3,a5,……, a2, a4, a6, …都是公差为3的等差数列.……………………1分
a1=-27, a1+a2==-51, a2=-24。采用叠加法可得,
当n为奇数时,an= ;…………………………3分
;…………………………3分
当n为偶数时,an= ……………………………5分
……………………………5分
∴an= ………………………………6分
………………………………6分
(2)因为n为偶数,所以
Sn=(a1+a2)+(a3+a4)+……+(an-1+an)…………………………8分
=(3×1-54)+(3×3?54)+……+[3(n?1)?54]
= …………………………………………10分
…………………………………………10分
若n为偶数,当n=18时,Sn取到最小值-243.……………………12分
20. (1)证明:∵PA⊥底面ABCD,∴PA⊥AD.
又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.……2分
又BC 平面PCB,∴平面PAB⊥平面PCB.……4分
平面PCB,∴平面PAB⊥平面PCB.……4分
(2)证明:∵PA⊥底面ABCD,∴PA⊥AD.
又PC⊥AD,∴AD⊥平面PAC,∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC= ,
,
∴∠DCA=∠BAC= .
.
又AC⊥AD,故△DAC为等腰直角三角形。
∴DC=2AB, 
 ……………………8分
……………………8分
(3)连结BD,交AC于点M,连结EM,则
在△BPD中, ∴PD∥EM.
∴PD∥EM.
又PD 平面EAC,EM
平面EAC,EM 平面EAC,
平面EAC,
∴PD∥平面EAC.……………………(12分)
21.解:(1)设直线AB的方程为y=k(x+1),
将y=k(x+1)代入x2+3y2=5, 消去y整理得(3k2+1)x2+6k2x+3k2-5=0.………2分
△=36k4-4(3k2+1)(3k2-5)>0恒成立,
设A(x1,y1), B(x2,y2), 则x1+x2= ,………………………………4分
,………………………………4分
由线段AB中点的横坐标是 ,
,
得 解得k=±
解得k=± .……………………5分
.……………………5分
所以直线AB的方程为 或
或 ……………………6分
……………………6分
(2)假设在x轴上存在点M(m, 0),使 为常数.
为常数.
由(1)知x1+x2= ①
①
所以
=
= ……………………8分
……………………8分
将①代入上式,整理得 ,
,
∴
∵
综上,在x轴上存在定点M ,使
,使 为常数……………………12分
为常数……………………12分
22.解:(1)f(x)的定义域为(0,+∞),f′(x)= ,
,
令f′(x)=0,得x=e1-a.……………………3分
当x∈(0, e1-a)时,f′(x)>0,f(x)在(0, e1-a)内是单调递增,当x∈(e1-a,+∞)时,f′(x)<0,f(x)在(e1-a,+∞)内是单调递减.…………………………6分
∴f(x)在x=e1-a处取得极大值f(e1-a)=ea-1.………………8分
(2)∵a>0, ∴e1-a<e2,∴[f(x)]max=f(e1-a)=ea-1,………………10分
∴f(x)的图象g(x)=1的图象在(0,e2]上有公共点,等价于ea-1≥1,……………12分
两边以e底取对数可解得a≥1,故a的取值范围是[1,+∞)……………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com