
选择题的解法
1.内容概要:
选择题注重考查基础知识、基本技能、基本方法、逻辑思维与直觉思维能力,以及观察、分析、比较、选择简捷运算方法的能力.
解答选择题的基本原则是小题不能大做,小题需小做、繁题会简做、难题要巧做。求解选择题的基本方法是以直接思路肯定为主,间接思路否定为辅,即求解时除了用直接计算方法之外还可以用逆向化策略、特殊化策略、图形化策略、整体化策略等方法求解.
解选择题要注意选择题的特殊性,充分利用题干和选择支两方面提供的信息,灵活、巧妙、快速求解.
2.典例精析
一、直接法:就是从题设条件出发,通过正确的运算、推理或判断,直接得出结论再与选择支对照,从而作出选择的一种方法.运用此种方法解题需要扎实的数学基础。
例1.(08浙江)若双曲线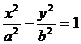 的两个焦点到一条准线的距离之比为
的两个焦点到一条准线的距离之比为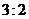 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
(A)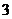 (B)
(B)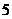 (C)
(C)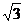 (D)
(D)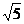
【解析】∵双曲线的准线为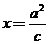 ,∴
,∴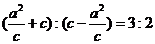 ,解得
,解得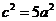 ,∴
,∴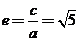 故选D.
故选D.
例2.设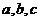 分别是
分别是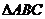 的三个内角
的三个内角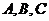 所对的边,则
所对的边,则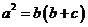 是
是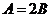 的( )
的( )
(A)充要条件 (B)充分而不必要条件
(C)必要而充分条件 (D)既不充分又不必要条件
【解析】设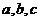 分别是
分别是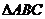 的三个内角
的三个内角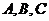 所对的边,若
所对的边,若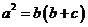 ,
,
则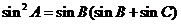 ,则
,则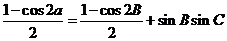 ,
,
∴ 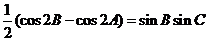 ,
,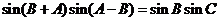 ,
,
又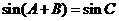 ,∴
,∴ 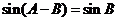 ,∴
,∴ 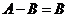 ,
,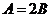 ,
,
若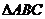 中,
中,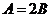 ,由上可知,每一步都可以逆推回去,得到
,由上可知,每一步都可以逆推回去,得到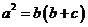 ,
,
所以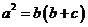 是
是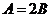 的充要条件,选A.
的充要条件,选A.
特例法主要包括:特殊值法、特殊函数法、特殊方程法、特殊数列法、特殊位置法、特殊点法等.
①特殊值法
二、特例法:就是运用满足题设条件的某些特殊数值、特殊位置、特殊关系、特殊图形、特殊数列、特殊函数等对各选择支进行检验或推理,利用问题在某一特殊情况下不真,则它在一般情况下也不真的原理,由此判明选项真伪的方法.用特例法解选择题时,特例取得愈简单、愈特殊愈好.
例3.(08全国Ⅱ)若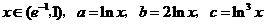 ,则( )
,则( )
A.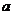 <
<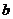 <
<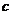 B.
B.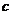 <
<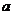 <
<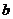 C.
C. 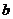 <
<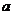 <
<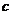 D.
D.
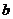 <
<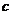 <
<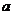
【解析】令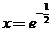 ,则
,则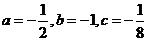 ,故选C.
,故选C.
例4.(08江西)若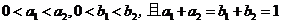 ,则下列代数式中值最大的是( )
,则下列代数式中值最大的是( )
A.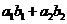 B.
B.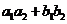 C.
C.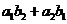 D.
D.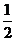
【解析】令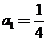 ,
,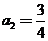 ,
,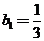 ,
,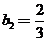 ,然后代入要比较大小的几个式子中计算即可,答案为A.
,然后代入要比较大小的几个式子中计算即可,答案为A.
【点评】从上面这些例子及其解答来看,2008年高考试题特别喜欢把大小比较与函数、三角等知识结合进行考查,这是2008年大小比较考题的一大亮点.
②特殊函数法
例5.如果奇函数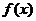 在[3,7]上是增函数且最小值为5,那么
在[3,7]上是增函数且最小值为5,那么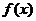 在区间[-7,-3]上是
( )
在区间[-7,-3]上是
( )
A. 增函数且最小值为-5 B. 减函数且最小值是-5
C. 增函数且最大值为-5 D. 减函数且最大值是-5
【解析】构造特殊函数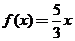 ,显然满足题设条件,并易知
,显然满足题设条件,并易知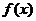 在区间[-7,-3]上是增函数,且最大值为
在区间[-7,-3]上是增函数,且最大值为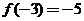 ,故选C.
,故选C.
③特殊数列法
例6. 已知等差数列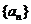 满足
满足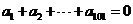 ,则有( )
,则有( )
A.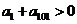 B.
B. C.
C.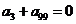 D.
D.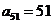
解析:取满足题意的特殊数列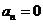 ,则
,则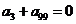 ,故选C.
,故选C.
④特殊方程法
例7.曲线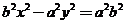 (
(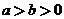 )的渐近线夹角为
)的渐近线夹角为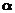 ,离心率为
,离心率为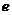 ,则
,则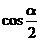 等于( )
等于( )
A.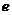 B.
B.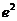 C.
C.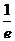 D.
D.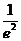
【解析】本题是考查双曲线渐近线夹角与离心率的一个关系式,故可用特殊方程来考察.取双曲线方程为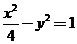 ,易得离心率
,易得离心率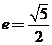 ,
,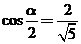 ,故选C.
,故选C.
⑤特殊位置法
例8.过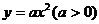 的焦点
的焦点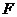 作直线交抛物线与
作直线交抛物线与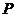 、
、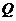 两点,若
两点,若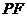 与
与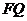 的长分别是
的长分别是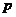 、
、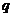 ,则
,则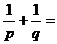 ( )
( )
A、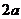 B、
B、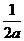 C、
C、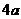 D、
D、 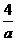
【解析】此抛物线开口向上,过焦点且斜率为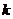 的直线与抛物线均有两个交点
的直线与抛物线均有两个交点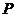 、
、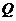 ,当
,当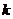 变化时
变化时 、
、 的长均变化,但从题设可以得到这样的信息:尽管
的长均变化,但从题设可以得到这样的信息:尽管 、
、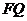 长度不定,但其倒数和应为定值,所以可以针对直线的某一特定位置进行求解,而不失一般性.
长度不定,但其倒数和应为定值,所以可以针对直线的某一特定位置进行求解,而不失一般性.
考虑直线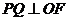 时,
时,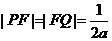 ,所以
,所以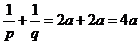 ,故选C.
,故选C.
⑥特殊点法
例9.(08全国Ⅰ)若函数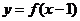 的图像与函数
的图像与函数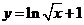 的图像关于直线
的图像关于直线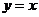 对称,则
对称,则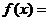 ( )
( )
A.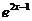 B.
B.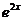 C.
C.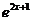 D.
D.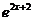
【解析】因为点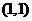 在
在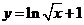 的图象上,它关于
的图象上,它关于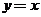 对称的点
对称的点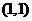 一定在其反函数
一定在其反函数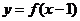 的图象上,即点
的图象上,即点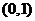 在函数
在函数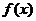 的图象上,将其代入四个选择支逐一检验,可以直接排除A、C、D,故选B.
的图象上,将其代入四个选择支逐一检验,可以直接排除A、C、D,故选B.
【点评】本题主要考查反函数的概念、函数与其反函数图象之间的关系、函数图象的平移.常规解法是先求出函数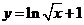 的反函数,然后再将函数图象平移即可得到正确解答.而本法抓住以下特征:函数图象上的点关于
的反函数,然后再将函数图象平移即可得到正确解答.而本法抓住以下特征:函数图象上的点关于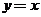 对称的点一定在其反函数的图象上,由此选定特殊点
对称的点一定在其反函数的图象上,由此选定特殊点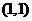 ,从而得出点
,从而得出点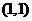 在
在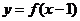 的图象上,进一步得出点
的图象上,进一步得出点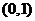 在
在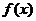 的图象上.于是快速求解.
的图象上.于是快速求解.
三、图解法:就是利用函数图像或数学结果的几何意义,将数的问题(如解方程、解不等式、求最值,求取值范围等)与某些图形结合起来,利用几何图形的直观几性,再辅以简单计算,确定正确答案的方法。
例10.函数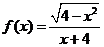 的最大值是( )
的最大值是( )
A.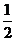 B.
B.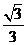 C.
C.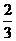 D.
D.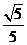
【解析】考察问题的几何意义:令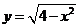 ,
, 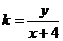 ,
,
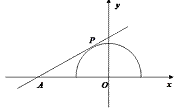
则直线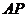 与半圆
与半圆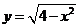 有公共点(如图所示),
有公共点(如图所示),
∴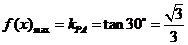 ,故选B.
,故选B.
【点评】本题主要考查函数最值的求法,以及逻辑思维能力和运算能力,侧重于考查观察、分析能力与思维的灵活性. 若能够仔细观察函数解析式的结构特征,发掘出隐藏在题目背后的丰富的数学“三基”,灵活运用有关知识,则可望速战速决,发现快捷解法――图解法.
例11.已知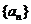 是等差数列,
是等差数列,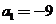 ,
,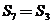 ,那么使其前n项和
,那么使其前n项和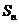 最小的n是( )
最小的n是( )
A. 4 B.
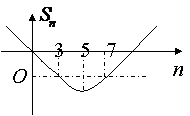 【解析】等差数列的前n项和
【解析】等差数列的前n项和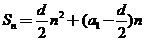 可表示为过原点的抛物线. 又本题中
可表示为过原点的抛物线. 又本题中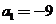 ,
,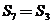 ,可表示如图.
,可表示如图.
由图可知,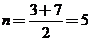 是抛物线的对称轴,
是抛物线的对称轴,
所以n=5时,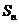 最小,故选B.
最小,故选B.
【点评】图解法(数形结合法)它体现了数形结合的思想,它是将函数、方程、不等式、甚至某些)式子,以图形表示后,再设法解决的基本方法。其思维形象直观、生动活泼,图解法要求我们不但能由“数”到“形”,而且还必须自觉地将“形”转化到“数”.
四、代入验证法:就是将选择支中给出的答案或其特殊值,代入题干逐一验证是否满足题设条件,然后选择符合题设条件的选择支的一种方法.
例12.函数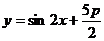 的图象的一条对称轴的方程是( )
的图象的一条对称轴的方程是( )
(A)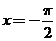 (B)
(B) 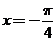 (C)
(C)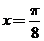 (D)
(D)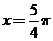
【解析】把选择支逐次代入,当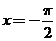 时,
时,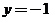 ,可见
,可见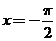 x=-是对称轴,又因为统一前提规定“只有一项是符合要求的”,故选A.
x=-是对称轴,又因为统一前提规定“只有一项是符合要求的”,故选A.
或直接法: ∵函数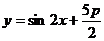 的图象的对称轴方程为
的图象的对称轴方程为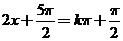 (
(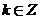 ),则
),则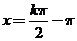 ,当
,当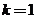 时,
时,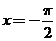 ,故选A.
,故选A.
【点评】代入法适应于题设复杂,结论简单的选择题.若能据题意确定代入顺序,则能较大提高解题速度.
五、筛选法:就是充分利用数学选择题是单选题的特征,从选择支入手,根据题设条件与各选择支之间的关系,通过分析、推理、计算、判断,对选择支进行筛选,将其中与题设相矛盾的干扰支逐一排除,从而获得正确结论的方法.
例13.给定四条曲线:①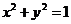 ,②
,②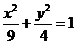 ,③
,③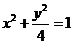 ,④
,④ 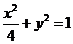 其中与直线
其中与直线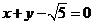 仅有一个交点的曲线是( )
仅有一个交点的曲线是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
【解析】分析选择支可知,四条曲线中有且只有一条曲线不符合要求,故可考虑找不符合条件的曲线从而筛选,而在四条曲线中,②是一个面积最大的椭圆,故可先看②,显然直线和曲线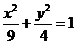 是相交的,因为直线上的点
是相交的,因为直线上的点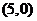 在椭圆内,对照选项,应选D.
在椭圆内,对照选项,应选D.
六、分析法:就是对有关概念进行全面、正确、深刻的理解或对有关信息提取、分析和加工后而作出判断和选择的方法.
分析法主要包括:特征分析法、逻辑分析法、直觉分析法等.
例14.设球的半径为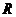 ,
,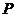 、
、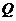 是球面上北纬
是球面上北纬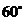 圈上的两点,这两点在纬度圈上的劣弧的长是
圈上的两点,这两点在纬度圈上的劣弧的长是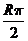 ,则这两点的球面距离是( )
,则这两点的球面距离是( )
例14.在题设条件中的△ABC的三边a、b、c满足等式acosA+bcosB=ccosC,则此三角形必是( )
A.以a为斜边的直角三角形 B.以b为斜边的直角三角形
C.等边三角形 D.其他三角形
【解析】题设条件中的等式是关于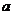 、A与
、A与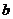 、B的对称式,因此选项在A、B为等价命题都被淘汰,若选项C正确,则有
、B的对称式,因此选项在A、B为等价命题都被淘汰,若选项C正确,则有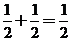 ,即
,即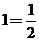 ,矛盾,从而C被淘汰,故选D.
,矛盾,从而C被淘汰,故选D.
例15.(07浙江)甲乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜,根据以往经验,每局比赛中甲获胜的概率为0.6,则本次比赛中甲获胜的概率为( )
A、0.216 B、0.36 C、0.432 D、0.648
【解析】先看“标准”解法――甲获胜分两种情况:①甲:乙=2:0,其概率为0.6×0.6=0.36,②甲:乙=2:1,其概率为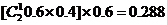 ,所以甲获胜的概率为0.36+0.288=0.648,选D.
,所以甲获胜的概率为0.36+0.288=0.648,选D.
现在再用直觉法来解:因为这种比赛没有平局,2人获胜的概率之和为1,而甲获胜的概率比乙大,应该超过0.5,只有选D.
【点评】当然有的题目不止用一种方法,需要几种方法同时使用;也有的题目有多种解法,这就需要在实际解题过程中去分析总结.
七、估算法:所谓估算法就是一种粗略的计算方法,利用“式”的放大或缩小,或“变量”的极端情况(如“端点”、“相等”、“极值点”和“极限状态”),对运算结果确定出一个范围或作出一个估计的方法.
例16.已知三棱锥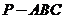 的侧面与底面所成二面角都是
的侧面与底面所成二面角都是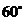 ,底面三角形三边长分别是7、8、9,则此三棱锥的侧面面积为( )
,底面三角形三边长分别是7、8、9,则此三棱锥的侧面面积为( )
A、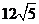 B、
B、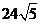 C、
C、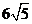 D、
D、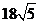
【解析】你可以先求出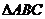 的面积为
的面积为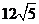 ,再利用射影面积公式求出侧面面积为
,再利用射影面积公式求出侧面面积为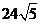 ;你也可以先求出
;你也可以先求出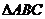 的面积为
的面积为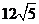 ,之后求出顶点
,之后求出顶点 在底面的射影到各侧面的距离,都是三棱锥
在底面的射影到各侧面的距离,都是三棱锥 的高的一半,再利用等体积法求得结果,但好象都不如用估值法:假设底面三角形三边长都是8,则面积为
的高的一半,再利用等体积法求得结果,但好象都不如用估值法:假设底面三角形三边长都是8,则面积为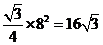 ,这个面积当然比原来大了一点点,再利用射影面积公式求出侧面面积为
,这个面积当然比原来大了一点点,再利用射影面积公式求出侧面面积为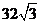 ,四个选项中只有
,四个选项中只有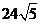 与之最接近,选B.
与之最接近,选B.
【总结提炼】从考试的角度来看,解选择题只要选对就行,至于用什么“策略”,“手段”都是无关紧要的.所以人称可以“不择手段”.但平时做题时要尽量弄清每一个选择支正确的理由与错误的原因,另外,在解答一道选择题时,往往需要同时采用几种方法进行分析、推理,只有这样,才会在高考时充分利用题目自身提供的信息,化常规为特殊,避免小题大作,真正做到准确和快速.
3.跟踪练习
1.函数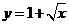 (
(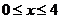 )的反函数是( )
)的反函数是( )
A.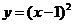 (
(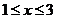 ) B.
) B.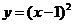 (
(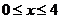 )
)
C.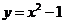 (
(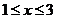 ) D.
) D.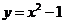 (
(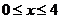 )
)
2.若实数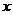 满足
满足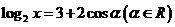 ,则
,则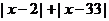 等于( )
等于( )
A.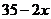 B.
B.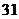 C.
C.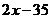 D.
D. 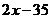 或
或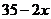
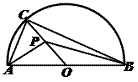 3.如图,半圆的直径
3.如图,半圆的直径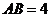 ,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则
,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则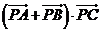 的最小值为( )
的最小值为( )
A.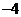 B.
B.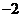 C.1 D.4
C.1 D.4
4.若椭圆的一个焦点是其三个顶点构成的三角形的垂心, 则椭圆的离心率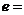 ( )
( )
A.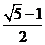 B.
B.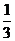 C.
C.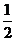 D.
D.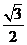
5.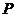 为正方形
为正方形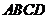 内一点,且
内一点,且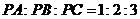 ,则
,则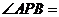 ( )
( )
A.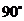 B.
B.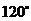 C.
C.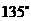 D.
D.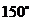
 6.如图,斜三棱柱
6.如图,斜三棱柱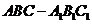 中,
中,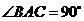 ,
,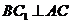 ,则
,则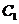 在底面
在底面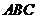 上的射影
上的射影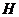 必在( )
必在( )
A.直线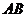 上 B. 直线
上 B. 直线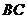 上
上
C. 直线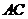 上 D.
上 D.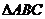 的内部
的内部
7.定点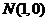 ,动点A、B分别在图中抛物线
,动点A、B分别在图中抛物线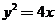 及椭圆
及椭圆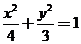 的实线上运动,且AB//x轴,则△NAB的周长
的实线上运动,且AB//x轴,则△NAB的周长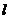 的取值范围是( )
的取值范围是( )
 A.(,2)
A.(,2)
B.(,4)
C.(,4)
D.(2,4)
8.用1,2,3,4,5,6组成没有重复数字的六位数,要求任何相邻2个数字的奇偶性不同,且1和2相邻,则这样的六位数的个数为( )
A.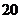 B.
B.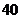 C.
C.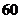 D.
D.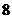
1. 由函数 知,当
知,当 时,
时, ,且
,且 ,则它的反函数过点(3,4),故选A.
,则它的反函数过点(3,4),故选A.
2.∵ ,∴
,∴ ,则
,则 ,即
,即 ,
, .
. ,选B.
,选B.
3. 由平行四边形法则, ,
,
∴ ,
,
又 ,
,
∴ ,当P为
,当P为 中点时,取得最小值
中点时,取得最小值 .选B.
.选B.
4. 设 是椭圆的一个焦点,它是椭圆三个顶点
是椭圆的一个焦点,它是椭圆三个顶点 ,
, ,
, 构成的三角形的垂心(如图).由
构成的三角形的垂心(如图).由 有
有 ,即
,即 ,∴
,∴ ,得
,得 ,解得
,解得 ,选A.
,选A.
5. 设正方形边长为 ,
, ,则
,则 ,
, .在
.在 由正弦定理得
由正弦定理得
 ,又在
,又在 由余弦定理得
由余弦定理得 ,于是
,于是 ,
, ,选C.
,选C.
 6.
6.  在底面
在底面 上的射影
上的射影 知,
知, 为斜线
为斜线 在平面
在平面 上的射影,∵
上的射影,∵ ,由三垂线定理得
,由三垂线定理得 ,∵
,∵ ,所以直线
,所以直线 与直线
与直线 重合,选A.
重合,选A.
7. 过A作抛物线 的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线
的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线 交右准线于
交右准线于 则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长
则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长 =|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
=|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
由可得两曲线的交点x=,xB∈(,2),
∴3+xB∈(,4),即△ANB周长 取值范围是(,4),选B.
取值范围是(,4),选B.
8. 先将3,5两个奇数排好,有 种排法,再将4,6两个偶数插入3,5中,有
种排法,再将4,6两个偶数插入3,5中,有 种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为
种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为 ,选B.
,选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com