
江苏省通州市2009届高三第六次调研测试
数学试卷
(考试时间:120分钟 满分160分)
一、填空题:本大题共14小题,每小题5分,共70分.
1.函数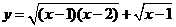 的定义域为 .
的定义域为 .
 2.已知复数与
2.已知复数与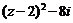 均为纯虚数,则等于 .
均为纯虚数,则等于 .
3.已知向量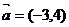 ,向量满足∥,且
,向量满足∥,且 ,则=
。
,则=
。
4.在等比数列{an}中,已知a4+a10=10,且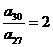 ,则= .
,则= .
5.已知命题:“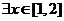 ,使x2+2x+a≥
,使x2+2x+a≥
范围是 .
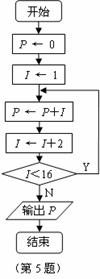
6.如图,程序执行后输出的结果为 .
7.下列命题正确的序号是_____ .
(其中l,m表示直线,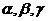 表示平面)
表示平面)
(1)若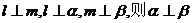 ; (2)若
; (2)若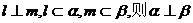 ;
;
(3)若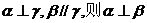 ;
(4)若
;
(4)若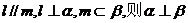
 8. 用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
8. 用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
则它的体积的最大值与最小值之差为 .
9.已知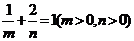 ,则当mn取得最小值时,椭圆
,则当mn取得最小值时,椭圆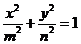 的离心率为
.
的离心率为
.
10.对任意两个集合A、B,定义: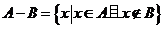 ,
,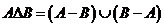 ,设
,设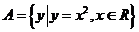 ,
,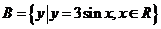 ,则
,则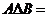
11.若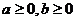 ,且当
,且当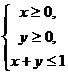 时,恒有
时,恒有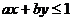 ,则以,b为坐标点
,则以,b为坐标点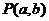 所形成的平面区域的面积等于 .
所形成的平面区域的面积等于 .
12.已知两个不共线的向量,的夹角为,且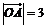 .若点M在直线OB上,且
.若点M在直线OB上,且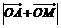 的最小值为,则的值为 .
的最小值为,则的值为 .
13.设函数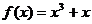 ,若
,若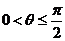 时,
时,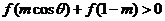 恒成立,则实数的取值范围是
_
.
恒成立,则实数的取值范围是
_
.
14.f(x)是定义在(0,+∞)上的非负可导函数,且满足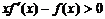 ,对任意正数a、b,若a<b,则
,对任意正数a、b,若a<b,则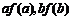 的大小关系为
.
的大小关系为
.
二、解答题:解答应写出文字说明,证明过程或演算步骤.
15.(本题满分14分)在△ABC中,角A、B、C的对边分别为a、b、c,若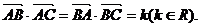
(1)判断△ABC的形状;
(2)若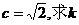 的值.
的值.
16.(本题满分14分)一个四棱锥的三视图和直观图如图所示,E为侧棱PD的中点.
(1)求证:PB//平面AEC;
17.(本题满分15分)已知圆A: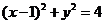 与轴负半轴交于B点,过B的弦BE与轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
与轴负半轴交于B点,过B的弦BE与轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
(1)求椭圆的方程;
(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值.
18.(本题满分15分)
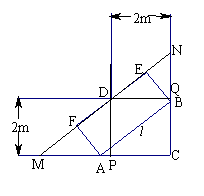
如图所示,一条直角走廊宽为
⑴若平板车卡在直角走廊内,且∠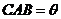 ,试求平板面的长 (用表示);
,试求平板面的长 (用表示);
⑵若平板车要想顺利通过直角走廊,其长度不能超过多少米?
19.(本题满分16分)已知数列的前n项和为,点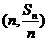 在直线
在直线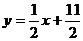 上.数列满足:
上.数列满足:
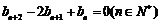 ,且
,且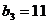 ,前9项和为153.
,前9项和为153.
(1)求数列,的通项公式;
(2)设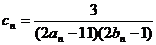 ,数列的前n项和为,求使不等式
,数列的前n项和为,求使不等式 对一切
对一切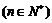 都成立的最大正整数的值;
都成立的最大正整数的值;
(3)设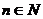 *,
*,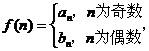 问是否存在
问是否存在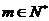 ,使得
,使得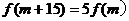 成立?若存在,求出的值;若不存在,请说明理由.
成立?若存在,求出的值;若不存在,请说明理由.
20.(本题满分16分)函数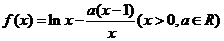 .
.
(1)试求f(x)的单调区间;
(2)当a>0时,求证:函数f(x)的图像存在唯一零点的充要条件是a=1;
(3)求证:不等式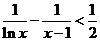 对于
对于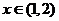 恒成立.
恒成立.
数学附加题
考试时间:30分钟 满分40分
分.每小题10分,共20分.解答时应写出文字说明、证明过程或演算过程.
一、选答题:本大题共4小题,请从这4题中选做2小题.如果多做,则按所做的前两题记
 1.(选修4一l:几何证明选讲)
1.(选修4一l:几何证明选讲)
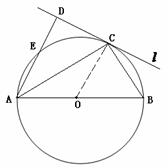
如图,圆O的直径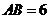 ,C为圆周上一点,
,C为圆周上一点,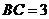 ,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D、E。求
,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D、E。求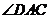 的度数与线段AE的长。
的度数与线段AE的长。
2.(选修4―2:矩阵与变换)
已知二阶矩阵A的属于特征值-1的一个特征向量为,属于特征值3的一个特征向量为,求矩阵A.
3.(选修4―4:坐标系与参数方程)
已知直线和参数方程为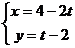
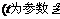 ,是椭圆
,是椭圆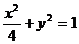 上任意一点,求点到直线的距离的最大值.
上任意一点,求点到直线的距离的最大值.
4.(选修4―5:不等式选讲)
已知f(x)=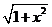 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
(1)求证: | f(x1)-f(x2)|≤| x1-x2| (2)若a2+b2=1,求证:f(a)+f(b) ≤.
选做题一:
选做题二:
二、必答题:本大题共2小题。每小题10分,共20分.解答时应写出文字说明、证明过程或演算过程.
 5. 将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b.设复数
5. 将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b.设复数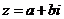 (i是虚数单位)。
(i是虚数单位)。
(1)求事件“为实数”的概率;
(2)求事件“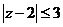 ”的概率。
”的概率。
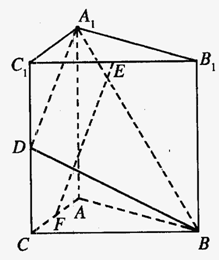
6. 如图,直三棱柱A1B
(1)求与平面A
(2) 求二面角B―A1D―A的平面角的正切值;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
江苏省通州市2009届高三第六次调研测试
一、填空题:本大题共14小题,每小题5分,共70分.
1. 2.2i 3.(
2.2i 3.( )或(
)或( ) 4.16 5.a≥-8 6.64 7.(1)(3)(4) 8.6 9. 10.
) 4.16 5.a≥-8 6.64 7.(1)(3)(4) 8.6 9. 10. 11.1 12.
11.1 12. 13.(-∞,1)
13.(-∞,1)
14. ,提示:设
,提示:设 ,则
,则 ,故
,故 为增函数,由a<b,有
为增函数,由a<b,有 ,也可以考虑特例,如f(x)=x2
,也可以考虑特例,如f(x)=x2
二、解答题:解答应写出文字说明,证明过程或演算步骤.
15.(1)

 5分
5分
即


 为等腰三角形. 8分
为等腰三角形. 8分
(2)由(I)知
 12分
12分

 14分
14分
16.(1)由图形可知该四棱锥和底面ABCD是菱形,且有一角为,边长为2,
锥体高度为1。
设AC,BD和交点为O,连OE,OE为△DPB的中位线,
OE//PB, 3分
EO面EAC,PB面EAC内, PB//面AEC。 6分
(2)过O作OFPA垂足为F ,
在Rt△POA中,PO=1,AO=,PA=2,在Rt△POB中,PO=1,BO=1,PB=, 8分
过B作PA的垂线BF,垂足为F,连DF,由于△PAB≌△PAD,故DF⊥PA,DF∩BF=F,因此PA⊥面BDF. 10分
在等腰三角形PAB中解得AF=,进而得PF=
即当 时,PA面BDF,
12分
时,PA面BDF,
12分
此时F到平面BDC的距离FH=
 14分
14分
17.(1) 4分
4分
椭圆方程为 7分
7分
(2) 10分
10分
 =2
14分
=2
14分
所以P在DB延长线与椭圆交点处,Q在PA延长线与圆的交点处,得到最大值为 . 15分
. 15分
18.(1)DM=,DN= ,MF=,EN=,
4分
,MF=,EN=,
4分
=EF=DM+DN-MF-EN=+ --
--
= (
( )
7分
)
7分
(2)“平板车要想顺利通过直角走廊”即对任意角( ),平板车的长度不能超过,即平板车的长度
),平板车的长度不能超过,即平板车的长度 ;记
;记
 ,有
,有 =
= ,
,
= =
= =,
10分
=,
10分
此后研究函数的最小值,方法很多;如换元(记 ,则
,则 )或直接求导,以确定函数在
)或直接求导,以确定函数在 上的单调性;当
上的单调性;当 时取得最小值
时取得最小值 。
15分
。
15分
19. (1)点(n,)在直线y=x+上,∴=n+,即Sn=n2+n,
an=n+5. 3分
∵bn+2-2bn+1+bn=0(nÎN*),∴bn+2-bn+1= bn+1-bn=…= b2-b1.
∴数列{bn}是等差数列,∵b3=11,它的前9项和为153,设公差为d,
则b1+2d=11,9b1+×d=153,解得b1=5,d=3.∴bn=3n+2. 6分
(2)由(1)得,cn= = =(-),
∴Tn=b1+b2+b3+…+bn=(1-)+(-)+(-)+…+(-)
=(1-). 9分
∵Tn=(1-)在nÎN*上是单调递增的,∴Tn的最小值为T1=.
∵不等式Tn>对一切nÎN*都成立,∴<.∴k<19.∴最大正整数k的值为18.11分
(3) nÎN*,f(n)==
当m为奇数时,m+15为偶数;当m为偶数时,m+15为奇数.
若f(m+15)=
或m+15+5=5(
解得m=11.所以当m=11时,f(m+15)=
20.(1) .
2分
.
2分
当时, ,在
,在 上单调递增;
3分
上单调递增;
3分
当时, 时,
时, ,在上单调递减;
,在上单调递减;
 时,
时, ,在
,在 上单调递增.
5分
上单调递增.
5分
综上所述,当时,的单调递增区间为 ;当时,的单调递增区间为
;当时,的单调递增区间为 ,单调递减区间为.
6分
,单调递减区间为.
6分
(2)充分性:a=1时,由(1)知,在x=1处有极小值也是最小值,
即 。而在上单调递减,在
。而在上单调递减,在 上单调递增,
上单调递增,
在 上由唯一的一个零点x=1.
9分
上由唯一的一个零点x=1.
9分
必要性: =0在 上有唯一解,且a>0, 由(1)知,在x=a处有极小值也是最小值f(a), f(a)=0,即
上有唯一解,且a>0, 由(1)知,在x=a处有极小值也是最小值f(a), f(a)=0,即 .
.
令 ,
,
 .
.
当 时,
时, ,在上单调递增;当a>1时,
,在上单调递增;当a>1时, ,
,
在 上单调递减。
上单调递减。 , =0只有唯一解a=1.
, =0只有唯一解a=1.
=0在 上有唯一解时必有a=1.
12分
上有唯一解时必有a=1.
12分
综上:在a>0时, =0在 上有唯一解的充要条件是a=1.
上有唯一解的充要条件是a=1.
(3)证明:∵1<x<2,∴ .
.
令 ,∴
,∴
 ,14分
,14分
由(1)知,当a=1时, ,∴
,∴ ,∴
,∴ .
.
∴ ,∴F(x)在(1,2)上单调递增,∴
,∴F(x)在(1,2)上单调递增,∴ ,
,
∴ 。∴
。∴ .
16分
.
16分
附加题答案
1.解:如图,连结OC,因 ,因此
,因此 ,由于
,由于 ,
,
 所以
所以 ,又
,又 得
得 ; 5分
; 5分
又因为 ,得
,得 ,那么
,那么 ,
,
从而 ,于是
,于是 。
10分
。
10分
2.解:设A= ,由题知
,由题知 =,
=, =3
=3
即 ,
5分
,
5分
∴ ∴A= 10分
10分
3.解: 直线的参数方程为 为参数)故直线的普通方程为
为参数)故直线的普通方程为 3分
3分
因为为椭圆 上任意点,故可设
上任意点,故可设 其中
其中 .
.
因此点到直线的距离是 7分
7分
所以当 ,时,取得最大值.
10分
,时,取得最大值.
10分
4. 证(1)
∵ ,
, ,
,
∴| f(x1)-f(x2)|<| x1-x2| 5分
(2) ,∴f(a)+f(b) ≤
,∴f(a)+f(b) ≤
∵
 ,
,
∴ 10分
10分
5.解:(1)为实数,即 为实数, ∴b=3
2分
为实数, ∴b=3
2分
又依题意,b可取1,2,3,4,5,6
故出现b=3的概率为
即事件“为实数”的概率为 5分
(2)由已知, 6分
6分
可知,b的值只能取1、2、3
当b=1时,  ,即a可取1,2,3
,即a可取1,2,3
当b=2时,  ,即a可取1,2,3
,即a可取1,2,3
当b=3时,  ,即a可取2
,即a可取2
由上可知,共有7种情况下可使事件“ ”成立 9分
”成立 9分
又a,b的取值情况共有36种
故事件“ ”的概率为
10分
”的概率为
10分
6.解:(1)∵A1B
∵AC⊥CB ∴BC⊥平面A
 ∴A1B与平面A
∴A1B与平面A 3分
3分
(2)分别延长AC,A1D交于G. 过C作CM⊥A
∵BC⊥平面ACC
∴BM⊥A
平面A
∴CG=2,DC=1 在直角三角形CDG中,

 ,
,
即二面角B―A1D―A的平面角的正切值为 6分
(3)在线段AC上存在一点F,使得EF⊥平面A1BD .
其位置为AC中点,证明如下:
∵A1B
∵由(1)BC⊥平面A
∵EF在平面A
同理可证EF⊥BD, ∴EF⊥平面A1BD
∵E为定点,平面A1BD为定平面,点F唯一 10分
解法二:(1)同解法一 3分
(2)∵A1B
C(0,0,0) B(2,0,0) A(0,2,0)
C1(0,0,2) B1(2,0,2) A1(0,2,2)
D(0,0,1) E(1,0,2)
 设平面A1BD的法向量为
设平面A1BD的法向量为


平面ACC
即二面角B―A1D―A的平面角的正切值为 6分
(3)在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD
欲使EF⊥平面A1BD 由(2)知,当且仅当//


∴存在唯一一点F(0,1,0)满足条件. 即点F为AC中点 10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com