
浙江省2008学年第二次五校联考
数学(理科)试题卷
参考公式 如果事件 、
、 互斥,那么
互斥,那么 .
.
如果事件 、
、 相互独立,那么
相互独立,那么 .
.
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么在
,那么在 次独立重复试验中恰好发生
次独立重复试验中恰好发生 次的概率
次的概率 .
.
锥柱的体积公式 柱体的体积公式
柱体的体积公式
其中 表示棱柱的底面积,
表示棱柱的底面积,  表示棱柱的高
表示棱柱的高
第Ⅰ卷(共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设全集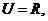 且
且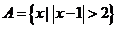 ,
,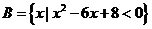 ,则
,则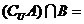 ( )
( )
(A)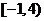 (B)
(B)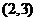 (C)
(C)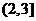 (D)
(D)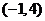
2.若复数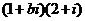 是纯虚数(
是纯虚数(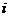 是虚数单位,
是虚数单位,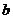 是实数),则
是实数),则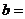 ( )
( )
(A)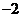 (B)
(B) (C)
(C)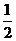 (D)2
(D)2
3. 椭圆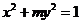 的焦点在
的焦点在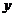 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则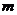 的值为( )
的值为( )
(A)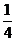 (B)
(B)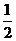 (C) 2 (D)4
(C) 2 (D)4
 4.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为( )
4.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为( )
(A) 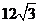 (B)
(B) 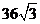 (C)
(C) 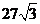 (D)6
(D)6
5.平面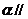 平面
平面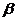 的一个充分条件是( )
的一个充分条件是( )
(A) 存在一条直线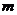 ,
, 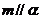 ,
,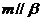 (B) 存在一条直线
(B) 存在一条直线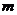 ,
, 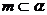 ,
,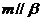
 (C) 存在两条平行直线
(C) 存在两条平行直线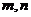 ,
, 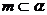
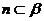 ,
,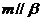 ,
,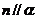
(D) 存在两条异面直线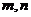 ,
,
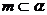
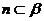 ,
,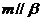 ,
,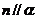
6.如图,该程序运行后输出的结果为( )
(A)36 (B)56 (C)55 (D)45
7.一个篮球运动员投篮一次得3分的概率为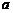 ,得2分的概率为
,得2分的概率为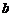 ,不得分的概率为
,不得分的概率为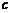 (
(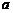 、
、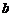 、
、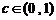 ),已知他投篮一次得分的数学期望为2(不计其它得分情况),则
),已知他投篮一次得分的数学期望为2(不计其它得分情况),则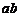 的最大值为( )
的最大值为( )
(A)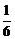 (B)
(B)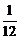
(C)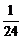 (D)
(D)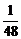
8. 在空间四边形ABCD中,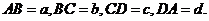 则
则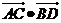 =( )
=( )
(A)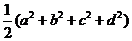 (B)
(B)
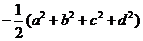
(C) 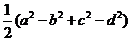 (D)
(D) 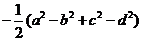
9.已知可导函数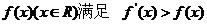 ,则当
,则当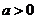 时,
时,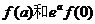 大小关系为( )
大小关系为( )
(A)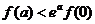 (B)
(B) 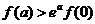 (C)
(C)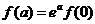 (D)
(D) 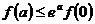
10.用砖砌墙,第一层(底层)用去了全部砖块的一半多一块,第二层用去了剩下的一半多一块, 依次类推,每一层都用去了前一层剩下的一半多一块,如果到第九层恰好砖用完,那么共用去砖的块数为
( )
依次类推,每一层都用去了前一层剩下的一半多一块,如果到第九层恰好砖用完,那么共用去砖的块数为
( )
(A)1018 (B)1020 (C)1022 (D)1024
第Ⅱ 卷(共100分)
二、填空题:本大题共7小题,每小题4分,共28分.
11.某校对全校男女学生共1600名进行健康调查,选用分层抽样法抽取一个容量为200的样本.已知女生比男生少抽了10人,则该校的女生人数应是 ▲ 人.
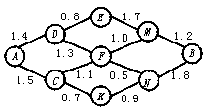 12. 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相连,连线上标注的数字表示某信息经过该段网线所需的时间(单位:毫秒).
12. 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相连,连线上标注的数字表示某信息经过该段网线所需的时间(单位:毫秒).
信息由结点A传递到结点B所需的最短时间为 ▲ 毫秒.
13.设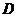 是不等式组
是不等式组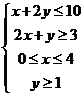 表示的平面区域,则
表示的平面区域,则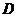 中的点
中的点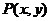 到直线
到直线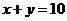 距离的最大值是 ▲ .
距离的最大值是 ▲ .
14.已知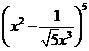 的展开式中的常数项为
的展开式中的常数项为 ,
,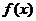 是以
是以 为周期的偶函数,且当
为周期的偶函数,且当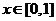 时,
时,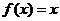 ,若在区间
,若在区间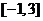 内,函数
内,函数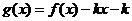 有4个零点,则实数
有4个零点,则实数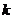 的取值范围是 ▲ .
的取值范围是 ▲ .
 15.在等差数列
15.在等差数列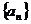 中,公差
中,公差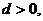
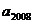 、
、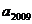 是方程
是方程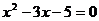 的两个根,
的两个根,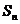 是数列
是数列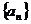 的前
的前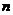 的和,那么满足条件
的和,那么满足条件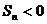 的最大自然数
的最大自然数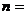 ▲ .
▲ .
16.如图给出16个点,其左和右相邻两点、上下相邻两点的距离都为1.若以这些点作为三角形的顶点,那么一共可得到 ▲ 个直角三角形.
17.设三角形ABC的BC边上的高AD=BC,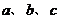 分别表示角A、B、C对应的三边,则
分别表示角A、B、C对应的三边,则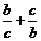 的取值范围是 ▲ .
的取值范围是 ▲ .
三、解答题
18. (本小题满分14分)已知向量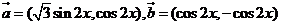 .
.
(Ⅰ)若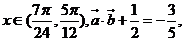 求
求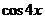 ;
;
(Ⅱ)设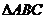 的三边
的三边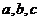 满足
满足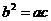 ,且边
,且边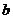 所对应的角为
所对应的角为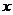 ,若关于
,若关于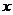 的方程
的方程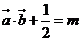 有且仅有一个实数根,求
有且仅有一个实数根,求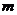 的值.
的值.
19. (本小题满分14分)袋中有6张卡片,编号分别是1,2,3,4,5,6.现在从袋中任意抽取出3张卡片,并记号码最大的为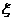 .
.
(Ⅰ)求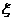 的分布列和期望;
的分布列和期望;
(Ⅱ)若3张卡片是有放回的抽取,则最大号码为4的概率是多少?
20. (本小题满分14分) 如图,在四棱锥P-ABCD中,PA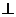 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
 (Ⅰ)试证:CD
(Ⅰ)试证:CD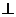 平面BEF;
平面BEF;
(Ⅱ)设PA=k?AB,且二面角E-BD-C的平面角大于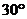 ,求k的取值范围.
,求k的取值范围.
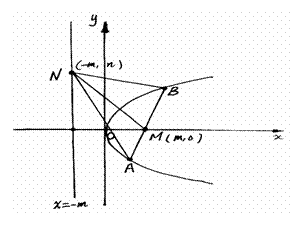
 21. (本小题满分15分)过抛物线
21. (本小题满分15分)过抛物线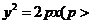
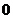
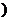 的对称轴上的定点
的对称轴上的定点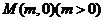 ,作直线
,作直线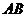 与抛物线相交于
与抛物线相交于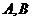 两点.
两点.
(Ⅰ)试证明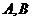 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(Ⅱ)若点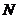 是定直线
是定直线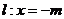 上的任意一点,分别记直线
上的任意一点,分别记直线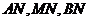 的斜率为
的斜率为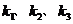 ,试探求
,试探求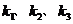 之间的关系,并给出证明.
之间的关系,并给出证明.
22. (本小题满分15分)设函数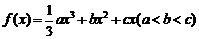 ,其图象在点
,其图象在点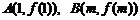 处的切线的斜率分别为
处的切线的斜率分别为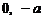 .
.
(Ⅰ)求证: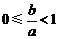 ;
;
(Ⅱ)若函数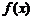 的递增区间为
的递增区间为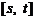 ,求
,求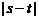 的取值范围;
的取值范围;
(Ⅲ)若当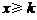 时(
时(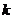 是与
是与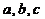 无关的常数),恒有
无关的常数),恒有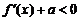 ,试求
,试求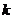 的最小值.
的最小值.
2008学年浙江省五校第二次联考
数学(理科)答案
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
D
D
A
D
B
C
二.填空题
11.760
12.4 .8
13.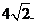 14.
14.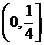
15.4015 16.184
17.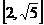
三.解答题
18.(Ⅰ)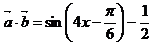 ……………..4分
……………..4分
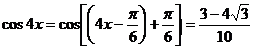 ……………..7分
……………..7分
(Ⅱ)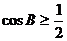 ,
,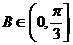 ……………..11分
……………..11分
结合图象可得: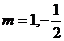 ……………..14分
……………..14分
19. (Ⅰ )
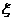
3
4
5
6
P
0.05
0.15
0.3
0.5
………………………………………………………………………………………….6分
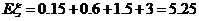 …………………………………………………….9分
…………………………………………………….9分
(Ⅱ)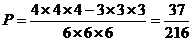 …………………………………………….14分
…………………………………………….14分
20.(Ⅰ)  解法一:
解法一:
(Ⅰ)证:由已知DF∥AB且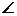 DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD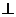 BF. ………..4分
BF. ………..4分
又PA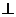 底面ABCD,CD
底面ABCD,CD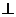 AD,故知CD
AD,故知CD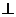 PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD
PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD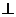 EF,由此得CD
EF,由此得CD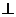 面BEF. ………..7分
面BEF. ………..7分
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,则在△PAC中易知EC∥PA.又因
PA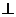 底面ABCD,故BC
底面ABCD,故BC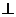 底面ABCD.在底面ABCD中,过C作GH
底面ABCD.在底面ABCD中,过C作GH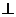 BD,垂足为H,连接EH.由三垂线定理知EH
BD,垂足为H,连接EH.由三垂线定理知EH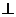 BD.从而
BD.从而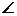 EHG为二面角E-BD-C的平面角. ………..10分
EHG为二面角E-BD-C的平面角. ………..10分
 设AB=a,则在△PAC中,有
设AB=a,则在△PAC中,有
BG=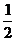 PA=
PA=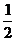 ka.
ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.
因S△CBD=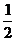 BD?GH=
BD?GH=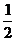 GB?OF.故GH=
GB?OF.故GH=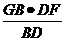 .
.
在△ABD中,因为AB=a,AD=2A,得BD=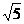 a
a
而GB=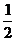 FB=
FB=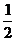 AD-a.DF-AB,从而得GH=
AD-a.DF-AB,从而得GH=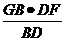 =
= 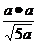 =
=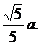 因此tanEHG=
因此tanEHG=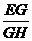 =
=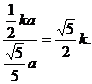 ………..12分
………..12分
由k>0知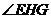 是锐角,故要使
是锐角,故要使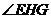 >
>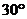 ,必须
,必须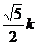 >tan
>tan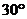 =
=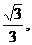
解之得,k的取值范围为k>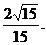 ………..14分
………..14分
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
 A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),
A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),
F(a,2a,0).
从而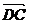 =(2a,0,0),
=(2a,0,0), 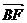 =(0,2a,0),
=(0,2a,0),
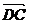 ?
?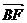 =0,故
=0,故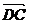
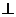
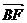 .
.
设PA=b,则P(0,0,b),而E为PC中点.故 第(20)
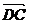 ?
?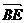 =0,故
=0,故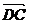
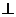
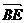 .
.
由此得CD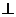 面BEF.
面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GH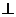 BD垂足为H,由三垂线定理知EH
BD垂足为H,由三垂线定理知EH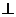 BD.
BD.
从而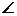 EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
由PA=k?AB得P(0,0,ka),E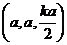 ,G(a,a,0).设H(x,y,0),则
,G(a,a,0).设H(x,y,0),则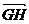 =(x-a,y-a,0),
=(x-a,y-a,0), 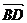 =(-a,2a,0),
=(-a,2a,0),
由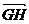 ?
?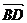 =0得=a(x-a)+2a(y-a)=0,即x-2y=-a ①
=0得=a(x-a)+2a(y-a)=0,即x-2y=-a ①
又因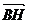 =(x,a,y,0),且
=(x,a,y,0),且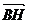 与
与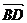 的方向相同,故
的方向相同,故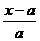 =
=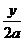 ,即2x+y=2a ②
,即2x+y=2a ②
由①②解得x=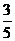 a,y=
a,y=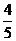 a,从而
a,从而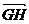 =
=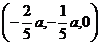 ,|
,|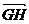 |=
|=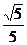 a.
a.
tanEHG=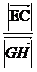 =
=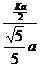 =
=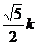 .由k>0知,EHC是锐角,由
.由k>0知,EHC是锐角,由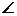 EHC>
EHC>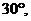 得tanEHG>tan
得tanEHG>tan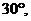 即
即
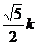 >
>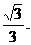 故k的取值范围为k>
故k的取值范围为k>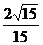 .
.
21.(1)证明:.设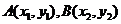 有
有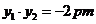 ,下证之:
,下证之:
设直线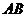 的方程为:
的方程为: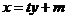 与
与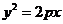 联立得
联立得
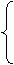
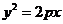
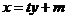 ,消去
,消去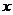 得
得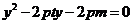 ……4分
……4分
由韦达定理得
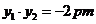 ,……6分
,……6分
 (2)解:三条直线
(2)解:三条直线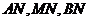 的斜率成等差数列,……9分
的斜率成等差数列,……9分
下证之:
设点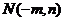 ,则直线
,则直线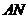 的斜率为
的斜率为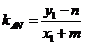 ;
;
直线 的斜率为
的斜率为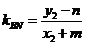
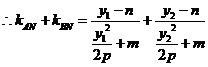
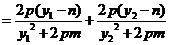
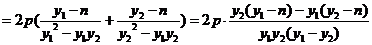
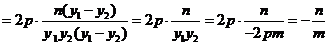 ……13分
……13分
又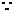 直线
直线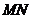 的斜率为
的斜率为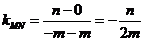 ……14分
……14分
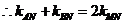 ,即直线
,即直线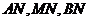 的斜率成等差数列. ……15分
的斜率成等差数列. ……15分
22. 解答:(1)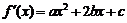 ,由题意及导数的几何意义得
,由题意及导数的几何意义得
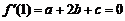 ,
, (1)
(1)
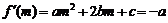 ,
(2) ……3分
,
(2) ……3分
又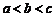 ,可得
,可得 ,即
,即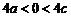 ,故
,故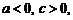 ……5分
……5分
由(1)得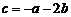 ,代入
,代入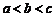 ,再由
,再由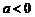 ,得
,得
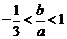 , (3) ……6分
, (3) ……6分
将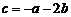 代入(2)得
代入(2)得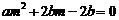 ,即方程
,即方程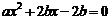 有实根.
有实根.
故其判别式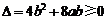 得
得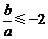 ,或
,或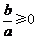 ,
(4) ……7分
,
(4) ……7分
由(3),(4)得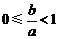 ;……8分
;……8分
(2)由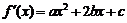 的判别式
的判别式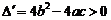 ,
,
知方程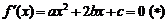 有两个不等实根,设为
有两个不等实根,设为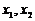 ,
,
又由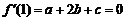 知,
知,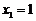 为方程(
为方程(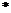 )的一个实根,则有根与系数的关系得
)的一个实根,则有根与系数的关系得
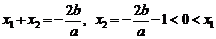 , …10分
, …10分
当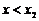 或
或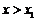 时,
时,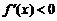 ,当
,当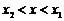 时,
时,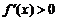 ,
,
故函数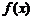 的递增区间为
的递增区间为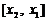 ,由题设知
,由题设知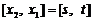 ,
,
因此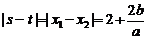 ,由(Ⅰ)知
,由(Ⅰ)知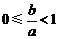 得
得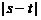 的取值范围为
的取值范围为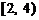 ;…12分
;…12分
(3)由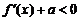 ,即
,即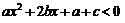 ,即
,即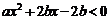 ,
,
因为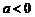 ,则
,则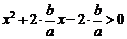 ,整理得
,整理得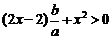 ,
,
设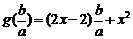 ,可以看作是关于
,可以看作是关于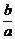 的一次函数,…13分
的一次函数,…13分
由题意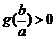 对于
对于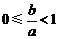 恒成立,
恒成立,
故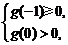 即
即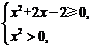 得
得 或
或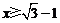 ,
,
由题意,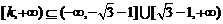 ,
,
故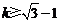 ,因此
,因此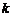 的最小值为
的最小值为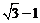 . …15分 www.1010jiajiao.com
. …15分 www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com