
题目列表(包括答案和解析)
(本小题满分13分)
 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
(I) 求这次铅球测试成绩合格的人数;
(II) 用此次测试结果估计全市毕业生的情况.若从 今年的高中毕业生中随机抽取两名,记![]() 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(III) 经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:
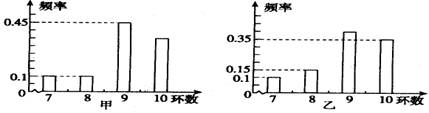
若将频率视为概率,回答下列问题:
(I)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(II)若甲、乙两运动员各自射击1次,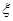 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求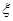 的分布列及
的分布列及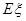 .
.
(本小题满分8分)已知函数 .
.
(I)求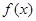 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(II)若锐角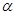 满足
满足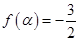 ,求角
,求角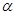 的值。
的值。
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下: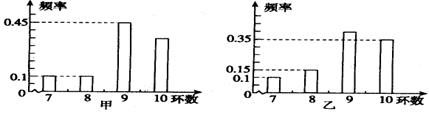
若将频率视为概率,回答下列问题:
(I)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(II)若甲、乙两运动员各自射击1次,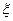 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求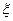 的分布列及
的分布列及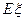 .
.
(本小题16分)已知各项均为实数的数列{an}是公差为d的等差数列,它的前n项和
为Sn,且满足S4=2S2+8.
(I)求公差d的值;
(II)若数列{an}的首项的平方与其余各项之和不超过10,则这样的数列至多有多少项;
(III)请直接写出满足(2)的项数最多时的一个数列(不需要给出演算步骤).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com