
题目列表(包括答案和解析)
(本小题满分14分)
阅读下面一段文字:已知数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,则易知通项
,则易知通项![]() ,前
,前![]() 项的和
项的和![]() . 将此命题中的“等号”改为“大于号”,我们得到:数列
. 将此命题中的“等号”改为“大于号”,我们得到:数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,那么
,那么![]() ,且
,且![]() . 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证
. 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证![]() ,可以先证
,可以先证![]() ,而要证
,而要证![]() ,只需证
,只需证![]() (
(![]() ). 结合以上思想方法,完成下题:
). 结合以上思想方法,完成下题:
已知函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,若数列
,若数列![]() 的前
的前![]() 项的和为
项的和为![]() ,求证:
,求证:![]() .
.
(本小题满分13分)已知函数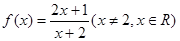 ,数列
,数列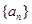 满足
满足
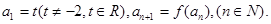
(1)若数列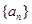 是常数列,求t的值;
是常数列,求t的值;
(2)当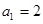 时,记
时,记 ,证明:数列
,证明:数列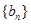 是等比数列,并求出通项公式an.
是等比数列,并求出通项公式an.
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
(本小题满分13分)已知函数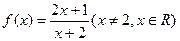 ,数列
,数列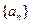 满足
满足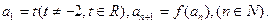
(1)若数列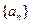 是常数列,求t的值;
是常数列,求t的值;
(2)当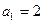 时,记
时,记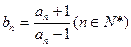 ,证明:数列
,证明:数列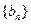 是等比数列,并求出通项公式an.
是等比数列,并求出通项公式an.
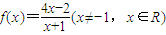 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com