
题目列表(包括答案和解析)
(本小题满分14分)(1)
(本小题满分7分)选修4-2:矩阵与变换
已知曲线 绕原点逆时针旋转
绕原点逆时针旋转 后可得到曲线
后可得到曲线 ,
,
(I)求由曲线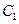 变换到曲线
变换到曲线 对应的矩阵
对应的矩阵 ;.
;.
(II)若矩阵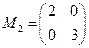 ,求曲线
,求曲线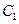 依次经过矩阵
依次经过矩阵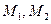 对应的变换
对应的变换 变换后得到的曲线方程.
变换后得到的曲线方程.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
已知直线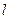 的参数方程为
的参数方程为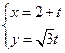 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为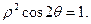
(1)求曲线C的直角坐标方程; (2)求直线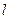 被曲线C截得的弦长.
被曲线C截得的弦长.
(本小题满分14分)(1)
(本小题满分7分)选修4-2:矩阵与变换
已知曲线 绕原点逆时针旋转
绕原点逆时针旋转 后可得到曲线
后可得到曲线 ,
,
(I)求由曲线 变换到曲线
变换到曲线 对应的矩阵
对应的矩阵 ;.
;.
(II)若矩阵 ,求曲线
,求曲线 依次经过矩阵
依次经过矩阵 对应的变换
对应的变换 变换后得到的曲线方程.
变换后得到的曲线方程.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为
(1)求曲线C的直角坐标方程; (2)求直线 被曲线C截得的弦长.
被曲线C截得的弦长.
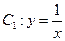 绕原点逆时针旋转
绕原点逆时针旋转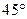 后可得到曲线
后可得到曲线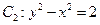 ,
,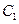 变换到曲线
变换到曲线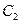 对应的矩阵
对应的矩阵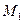 ;.
;.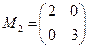 ,求曲线
,求曲线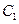 依次经过矩阵
依次经过矩阵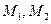 对应的变换
对应的变换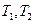 变换后得到的曲线方程.
变换后得到的曲线方程.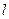 的参数方程为
的参数方程为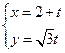 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为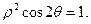
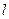 被曲线C截得的弦长.
被曲线C截得的弦长.(本题是选做题,满分28分,请在下面四个题目中选两个作答,每小题14分,多做按前两题给分)
A.(选修4-1:几何证明选讲)
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
B.(选修4-2:矩阵与变换)
在直角坐标系中,已知椭圆 ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积.
C.(选修4-4:坐标系与参数方程)
直线 (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.
D.(选修4-5:不等式选讲)
设 ,求证:
,求证: .
.
|
| ξ |
|
| ξ |
| ξ2 |
| ξ |
|
| π |
| 4 |
| 2 |
| 1 |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com