某校高三数学竞赛初赛考试后，对考生的成绩进行统计（考生成绩均不低于90分，满分150分），将成绩按如下方式分成六组，第一组[90，100）、第二组[100，110）…第六组[140，150]．图（1）为其频率分布直方图的一部分，若第四、五、六组的人数依次成等差数列，且第六组有4人．
（Ⅰ）请补充完整频率分布直方图，并估计这组数据的平均数M；

（Ⅱ）若不低于120分的同学进入决赛，不低于140分的同学为种子选手，完成下面2×2
列联表（即填写空格处的数据），并判断是否有99%的把握认为“进入决赛的同学
成为种子选手与专家培训有关”．

	a≥- 1 2	[140，150]	合计
参加培训	5		8
未参加培训
合计		4

附：K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

P（K2≥k0）	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k0	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

某服装商场为了了解毛衣的月销售量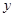(件)与月平均气温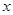(℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：

月平均气温	17	13	8	2
月销售量（件）	24	33	40	55

（1）做出散点图；

(2) 求线性回归方程 ；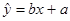

(3)气象部门预测下个月的平均气温约为6ºC，据此估计该商场下个月毛衣的销售量．（   ,）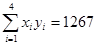

 

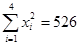某服装商场为了了解毛衣的月销售量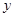(件)与月平均气温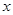(℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：

月平均气温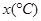	17	13	8	2
月销售量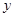（件）	24	33	40	55

（1）做出散点图；
(2) 求线性回归方程 ；
(3)气象部门预测下个月的平均气温约为6ºC，据此估计该商场下个月毛衣的销售量．（   ,）

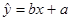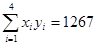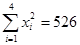某高校共有学生15 000人，其中男生10 500人，女生4 500人，为调查该校学生每周平均体育运动的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．
（1）应收集多少位女生的样本数据？
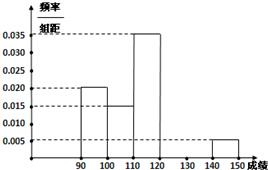
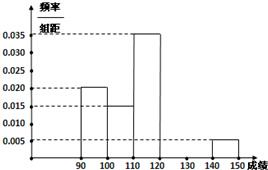
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为：[0,2],(2,4], (4,6], (6,8], (8,10], (10,12],估计该校学生每周平均体育运动时间超过4小时的概率；

（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
附：

P(K2≥k0)	0.10	0.05	0.010	0.005
k0	2.706	3.841	6.635	7.879