练习册

  • 练习册
  • 试题
    20．为了研究吸烟是否与性别有关.随机对100名成年人进行了问卷调查.经过计算得 的观测值为8.333.则有 的把握确定吸烟与性别有关. 下面的临界表供参考: 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 【查看更多】

     

    题目列表(包括答案和解析)

    为了研究吸烟是否与患肺癌有关，对50位肺癌患者及50位非肺癌患者．调查了其中吸烟的人数，得下列2×2列联表，试问：我们有多大的把握说吸烟与患肺癌有关？
    患肺癌 不患肺癌 合计
    吸烟 40 10 50
    不吸烟 10 40 50
    合计 50 50 100
    k2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    n=a+b+c+d
    P（K2≥k0） 0.05 0.025 0.010 0.005 0.001
    k0 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    为了研究吸烟是否与患肺癌有关，对50位肺癌患者及50位非肺癌患者．调查了其中吸烟的人数，得下列2×2列联表，试问：我们有多大的把握说吸烟与患肺癌有关？
    患肺癌不患肺癌合计
    吸烟401050
    不吸烟104050
    合计5050100
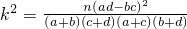    数学公式n=a+b+c+d
    P（K2≥k0）0.050.0250.0100.0050.001
    k03.8415.0246.6357.87910.828

    查看答案和解析>>

    为了研究吸烟是否与患肺癌有关，对50位肺癌患者及50位非肺癌患者．调查了其中吸烟的人数，得下列2×2列联表，试问：我们有多大的把握说吸烟与患肺癌有关？
    患肺癌不患肺癌合计
    吸烟401050
    不吸烟104050
    合计5050100
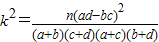    n=a+b+c+d
    P（K2≥k）0.050.0250.0100.0050.001
    k3.8415.0246.6357.87910.828

    查看答案和解析>>

    某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：
    专业
    性别    		 非统计专业 统计专业
    男 13 10
    女 7 20
    为了判断主修统计专业是否与性别有关系，根据表中的数据，计算得到Χ2=
    4.844
    4.844
    （保留三位小数），所以判定
    有
    有
    （填“有”或“没有”）95%的把握认为主修统计专业与性别有关系．

    查看答案和解析>>

    为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：
                        性别
    是否需要志愿者         		男 女
    需要 40  30
    不需要 160  270
    为了检验该地区的老年人需要志愿者提供帮助是否与性别有关系，根据表中数据，得到Χ2≈9.967，所以断定该地区的老年人需要志愿者提供帮助与性别有关系，这种判断出错的 可能性为（　　）
    参考数据：
    P（Χ2≥k） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>


    同步练习册答案