（本题满分10分）在一个口袋中装有12个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球，得到红球的概率是，从袋中任意摸出2个球，至少得到一个黑球的概率是。

求：（1）袋中黑球的个数；

（2）从袋中任意摸出3个球，至少得到2个黑球的概率。（结果用分数表示）

(本小题满分12分)一个袋子中有红、白、蓝三种颜色的球共24个，除颜色外完全相同，已知蓝色球3个. 若从袋子中随机取出1个球，取到红色球的概率是.

(1)求红色球的个数；

(2)若将这三种颜色的球分别进行编号，并将1号红色球，1号白色球，2号蓝色球和3号蓝色球这四个球装入另一个袋子中，甲乙两人先后从这个袋子中各取一个球(甲先取，取出的球不放回)，求甲取出的球的编号比乙的大的概率．

(本小题满分12分)一个袋子中有红、白、蓝三种颜色的球共24个，除颜色外完全相同，已知蓝色球3个. 若从袋子中随机取出1个球，取到红色球的概率是.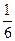
(1)求红色球的个数；
(2)若将这三种颜色的球分别进行编号，并将1号红色球，1号白色球，2号蓝色球和3号蓝色球这四个球装入另一个袋子中，甲乙两人先后从这个袋子中各取一个球(甲先取，取出的球不放回)，求甲取出的球的编号比乙的大的概率．

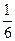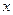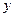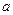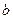（本小题满分12分）甲有一个装有个红球、个黑球的箱子，乙有一个装有个红球、个黑球的箱子，两人各自从自己的箱子里任取一球，并约定:所取两球同色时甲胜，异色时乙胜（，，，）．
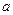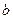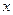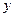
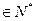(Ⅰ)当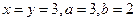,时，求甲获胜的概率；
（Ⅱ）当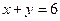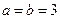，时，规定：甲取红球获胜得3分；取黑球获胜得1分；甲负得0分．求甲的得分期望达到最大时的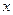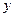，值；
（Ⅲ）当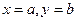时，这个游戏规则公平吗？请说明理由．