练习册

  • 练习册
  • 试题
    2．经典回放: 例1: 要从甲乙两名跳远运动员中选拔一名去参加运动会.选拔的标准是:先看他们的平均成绩.如果两人的平均成绩相差无几.就要再看他们成绩的稳定程度.为此对两人进行了15次比赛.得到如下数据:: 甲 755 752 757 744 743 729 721 731 778 768 761 773 764 736 741 乙 729 767 744 750 745 753 745 752 769 743 760 755 748 752 747 如何通过对上述数据的处理.来作出选人的决定呢? 解:甲≈750.2 乙≈750.6 s甲≈16.4 s乙≈9.6 甲乙两名跳远运动员的平均成绩相差无几.乙的成绩较稳定.所以选拔乙去参加运动会比较合适. 点评:总体平均数描述一总体的平均水平.方差和标准差描述数据的波动情况或者叫稳定程度. 例2:证明方差的两个性质 ①．若给定一组数据.方差为s2.则的方差为 ②．若给定一组数据.方差为s2.则的方差为, 解:设一组样本数据.其平均数为=.则 样本方差:s2=((x1-)2+(x2-)2+-+(xn-)2) 另一组样本数据.其平均数为=a,则 样本方差=((ax1-a)2+(ax2-a)2+-+(axn-a)2) =a2((x1-)2+(x2-)2+-+(xn-)2) =. 同样:另一组样本数据.其平均数为 =a+b, 样本方差=((ax1+b-a-b)2+(ax2+b-a-b)2+-+(axn+b-a-b)2) = a2((x1-)2+(x2-)2+-+(xn-)2) =. 点评:特别地.当时.则有的方差为s2.这说明将一组数据的每一个数据都减去相同的一个常数.其方差是不变的.即不影响这组数据的波动性. [同步训练] 【查看更多】

     

    题目列表(包括答案和解析)

    要从甲,乙两名运动员中选拔一人参加2012年伦敦奥运会跳水项目,对甲乙两人进行培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出成绩茎叶图如图所示.

    (1)从平均成绩及发挥稳定性的角度考虑,你认为选派哪名运动员更合适?

    (2)若将频率视为概率,对甲运动员在今后3次的比赛成绩进行预测,记这3次成绩中高于80分的次数为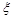,求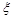的分布列及数学期望.

     

    查看答案和解析>>

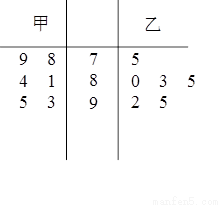
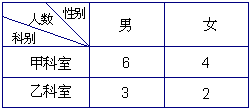    某单位甲乙两个科室人数及男女工作人员分布情况见右表．现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查．
    （1）求从甲、乙两科室各抽取的人数；
    （2）求从甲科室抽取的工作人员中至少有1名女性的概率；
    （3）记ξ表示抽取的3名工作人员中男性的人数，求ξ的分布列及数学期望．

    查看答案和解析>>

    已知甲口袋中有8个大小相同的小球，其中有5个白球，3个黑球；乙口袋中有4个大小相同的小球，其中有2个白球，2个黑球．现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两个口袋中共摸出3个小球．
    （I ）求从甲、乙两个口袋中分别抽取小球的个数；
    （II ）求从甲口袋中抽取的小球中恰有一个白球的概率；
    （III）求抽取的3个小球中只有一个黑球的概率．

    查看答案和解析>>

    某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人．现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽取3名工人进行技术考核．
    （1）求从甲、乙两组各抽取的人数；
    （2）记ξ表示抽取的3名工人中男工人数，求ξ的分布及数学期望．

    查看答案和解析>>

    某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人，现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽取3名工人进行技术考核．
    （Ⅰ）求从甲、乙两组各抽取的人数；
    （Ⅱ）求从甲组抽取的工人中恰有1名女工人的概率；
    （Ⅲ）记ξ表示抽取的3名工人中男工人数，求ξ的分布列及数学期望．

    查看答案和解析>>


    同步练习册答案