练习册

  • 练习册
  • 试题
    算筹.算盘.计算机等从古到今计算工具的变化.现了中国古代数学与现代计算机科学的联系.它们的基础都是“算法 . 算法这个名词虽然听起来很陌生.但它确是一个古老的概念.我们却从小学就开始接触算法.如.做四则运算要先乘除后加减.从里往外脱括弧.竖式笔算等都是算法.至于乘法口诀.珠算口诀更是算法的具体体现.广义地说.算法就是做某一件事的步骤或程序.现代科学研究的三大支柱是科学计算.科学实验.理论研究.算法的研究和应用正是本课程的主题 ! 【查看更多】

     

    题目列表(包括答案和解析)

    （08年吉林一中文） （12分）某种考试一共有5道题，考试时计算机随机从这5道题中抽取3道题来考试，全部答对才算合格。某人只会答其中的4道题，另一道题不会答。

        （1）求这个人只参加一次考试就合格的概率；

    （2）在上述条件都不变的情况下，某人可以连续参加不超过3次的这样的考试（每次考试，题中的条件都不发生变化），求他考试合格的概率。

    查看答案和解析>>

    据我国古书《唐阙史》记载，公元855年前后，有一次，青州府要从两个办事员中选拔一人当官，但是这两个办事员的职务、资历、能力和成绩，表现并无显著的差异，而名额只有一个，提升谁？负责提升的官员感到十分为难，就去请教青州的地方官杨埙．杨埙考虑了很久，想出了一个主意，他说：“官员应该能写会算，你把他们叫来，我出一道题当场考考他们，谁先算出就提升谁．”同时，杨埙让人把他出的题抄成两份，负责提升的官员找来两位办事员，给每人一袋算筹，一声令下两个人开始解题，不一会儿，其中一个先算出了正确答案，杨埙当场宣布提升他．大家都认为杨埙这种办法比较公允．在古代，像这样用“数学竞赛”来决定官员晋升是为数不少的．题目的大意如下：

    一天夜里，有一个人在林中散步，无意中听到几个强盗在商量怎样分配抢来的布匹，只听见他们说：“如果每人分6匹，就剩5匹；如果每人分7匹，就差8匹．”问有强盗几个？布匹多少？能用一个简单算法求出强盗个数和布匹数吗？

    查看答案和解析>>

    研究统计问题的基本思想方法是（　　）

    查看答案和解析>>

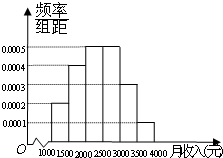    （2012•梅州二模）一个社会调查机构就某社区居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图（如图）．
    （1）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，求月收入在[1500，2000）（元）段应抽出的人数；
    （2）为了估计该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率，采用随机模拟的方法：先由计算器算出0到9之间取整数值的随机数，我们用0，1，2，3，…表示收入在[2000，3000）（元）的居民，剩余的数字表示月收入不在[2000，3000）（元）的居民；再以每三个随机数为一组，代表统计的结果，经随机模拟产生了20组随机数如下：
    907  966  191  925  271  932  812  458
    569  683  431  257  393  027  556  488
    730  113  537  989
    据此估计，计算该社区3个居民中恰好有2个月收入在[2000，3000）（元）的概率．
    （3）任意抽取该社区6个居民，用ξ表示月收入在（2000，3000）（元）的人数，求ξ的数学期望．

    查看答案和解析>>

    （2011•许昌一模）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．

    （Ⅰ）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，求月收入在[1500，2000）（元）段应抽出的人数；
    （Ⅱ）为了估计该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率，采用随机模拟的方法：先由计算器算出0到9之间取整数值的随机数，我们用0，1，2，3，4，…，表示月收入在[2000，3000）（元）的居民，剩余的数字表示月收入不在[2000，3000）（元）的居民；再以每三个随机数为一组，代表统计的结果．经随机模拟产生了20组随机数如下：
    907    966    191    925    271    932    812    458    569    683
    431    257    393    027    556    488    730    113    537    989
    据此估计，计算该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率．

    查看答案和解析>>


    同步练习册答案