(本小题满分16分)

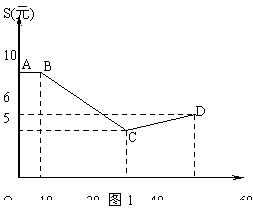
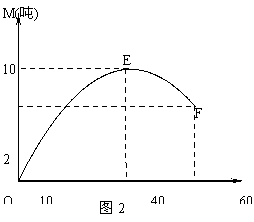
时值5月，荔枝上市．某市水果市场由历年的市场行情得知，从5月10日起的60天内，荔枝的售价S(t)(单位：元／kg)与上市时间t(单位：天)的关系大致可用如图1所示的折线ABCD表示，每天的销售量M(t)(单位：吨)与上市时间t(单位：天)的关系大致可用如图2所示的抛物线段OEF表示，其中O为坐标原点，E是抛物线的顶点．

（1）请分别写出S(t)，M(t)关于t的函数关系式；

（2）在这60天内，该水果市场哪天的销售额最大？

(选修4-4：坐标系与参数方程) （本小题满分10分）

在直角坐标系xoy中，直线的参数方程为（t为参数）,在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为.

（Ⅰ）求圆C的直角坐标方程；

（Ⅱ）设圆C与直线交于点A、B，若点P的坐标为，求|PA|+|PB|.

23（本小题满分10分）

 已知三棱锥P－ABC中，PA⊥平面ABC，AB⊥AC，，N为AB上一点，AB=4AN, M、S分别为PB,BC的中点.以A为原点，射线AB，AC，AP分别为x，y，z轴正向建立如图空间直角坐标系.

（Ⅰ）证明：CM⊥SN；

（Ⅱ）求SN与平面CMN所成角的大小.

24．（本小题满分10分）

将一枚硬币连续抛掷次，每次抛掷互不影响. 记正面向上的次数为奇数的概率为，正面向上的次数为偶数的概率为.

 （Ⅰ）若该硬币均匀，试求与；

 （Ⅱ）若该硬币有暇疵，且每次正面向上的概率为，试比较与的大小.

(选修4-4：坐标系与参数方程) （本小题满分10分）

在直角坐标系xoy中，直线的参数方程为（t为参数）,在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为.

（Ⅰ）求圆C的直角坐标方程；

（Ⅱ）设圆C与直线交于点A、B，若点P的坐标为，求|PA|+|PB|.

23（本小题满分10分）

 已知三棱锥P－ABC中，PA⊥平面ABC，AB⊥AC，，N为AB上一点，AB=4AN, M、S分别为PB,BC的中点.以A为原点，射线AB，AC，AP分别为x，y，z轴正向建立如图空间直角坐标系.

（Ⅰ）证明：CM⊥SN；

（Ⅱ）求SN与平面CMN所成角的大小.

24．（本小题满分10分）

将一枚硬币连续抛掷次，每次抛掷互不影响. 记正面向上的次数为奇数的概率为，正面向上的次数为偶数的概率为.

 （Ⅰ）若该硬币均匀，试求与；

 （Ⅱ）若该硬币有暇疵，且每次正面向上的概率为，试比较与的大小.

A．选修4－1：几何证明选讲

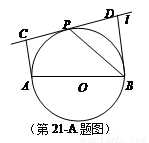
如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC＝PD．求证：（1）l是⊙O的切线；（2）PB平分∠ABD．

B．选修4－2：矩阵与变换

（本小题满分10分）

已知点A在变换：T：→＝作用后，再绕原点逆时针旋转90°，得到点B．若点B坐标为(－3，4)，求点A的坐标．

C．选修4－4：坐标系与参数方程

（本小题满分10分）

求曲线C1：被直线l：y＝x－所截得的线段长．

D．选修4－5：不等式选讲

（本小题满分10分）

已知a、b、c是正实数，求证：≥．

本小题满分10分）选修4—4：坐标系与参数方程
如图，已知点，，圆是以为直径的圆，直线：（为参数）．

（Ⅰ）写出圆的普通方程并选取适当的参数改写为参数方程；
（Ⅱ）过原点作直线的垂线，垂足为，若动点满足，当变化时，求点轨迹的参数方程，并指出它是什么曲线．