
题目列表(包括答案和解析)
.(本小题满分12分)设命题![]() :关于
:关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ;命题
;命题![]() :函数
:函数![]() 的值域是
的值域是![]() .如果命题
.如果命题![]() 和
和![]() 有且仅有一个正确,求实数
有且仅有一个正确,求实数![]() 的取值范围.
的取值范围.
(本小题满分12分)(1)对于定义在 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若 是定义在
是定义在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 上的减函数。然后填空建立一个普遍化的命题
上的减函数。然后填空建立一个普遍化的命题 :
:
设 是定义在
是定义在 上的可导函数,
上的可导函数, ,若
,若  +
+
 ,
,
则 是 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
(本小题满分12分)设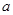 是实数,对函数
是实数,对函数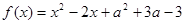 和抛物线
和抛物线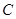 :
: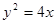 ,有如下两个命题:
,有如下两个命题: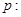 函数
函数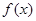 的最小值小于0;
的最小值小于0; 抛物线
抛物线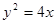 上的点
上的点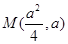 到其准线的距离
到其准线的距离 .
.
已知“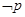 ”和“
”和“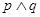
 ”都为假命题,求
”都为假命题,求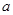 的取值范围.
的取值范围.
(本小题满分12分)(1)对于定义在 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若 是定义在
是定义在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 上的减函数。然后填空建立一个普遍化的命题:
上的减函数。然后填空建立一个普遍化的命题:
设 是定义在
是定义在 上的可导函数,
上的可导函数, ,若
,若  +
+
 ,
,
则
是 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
本小题满分12分)
设命题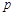 :函数f(x)=x3-ax-1在区间
:函数f(x)=x3-ax-1在区间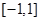 上单调递减;命题
上单调递减;命题 :函数
:函数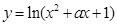 的定义域是
的定义域是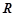 .如果命题
.如果命题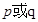 为真命题,
为真命题,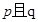 为假命题,求
为假命题,求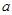 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com