
题目列表(包括答案和解析)
 某地区50位居民的人均月用水量(单位:t)的分组及频数如下:
某地区50位居民的人均月用水量(单位:t)的分组及频数如下:| 分组 | 频数 | 频率 |
| [1,2) | 5 | |
| [2,3) | 10 | |
| [3,4) | 20 | |
| [4,5) | 15 |
|
| 分组 | 151.5~158.5 | 158.5~165.5 | 165.5~172.5 | 172.5~179.5 |
| 频数 | 6 | 21 | m | |
| 频率 | a | 0.1 |
有一个容量为100的样本,数据的分组及各组的频数如下: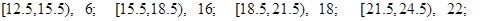

(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图;(3)由直方图确定样本的中位数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com